NCERT Solutions for Class 6 Maths Chapter 13 Symmetry
Here, you will get Chapter 13 Symmetry NCERT Solutions for Class 6 Maths which is quite helpful improving the marks in the examinations and have edge over your classmates. You can download PDF of Class 6 Maths NCERT Solutions Chapter 13 Symmetry which serve as beneficial tool that can be used to recall various questions any time. These NCERT Solutions will become your comprehensive guide in easy learning and evaluating yourself.
Class 6 Maths help in building a great foundation of concepts and make easy for the students to understand basics. It will make you understand the topics in most simple manner and grasp it easily to perform better. Students should also refer previous year questions and practise test papers and worksheets to assess their key areas.

Exercise 13.1
1. List any four symmetrical objects from your home or school.
Answer
Notebook, Blackboard, Glass, Inkpot.
2. For the given figure, which one is the mirror line, l1 or l2?

Answer
l2 is the mirror line as both sides of the lines are symmetric.
3. Identify the shapes given below. Check whether they are symmetric or not. Draw the line of symmetry as well.
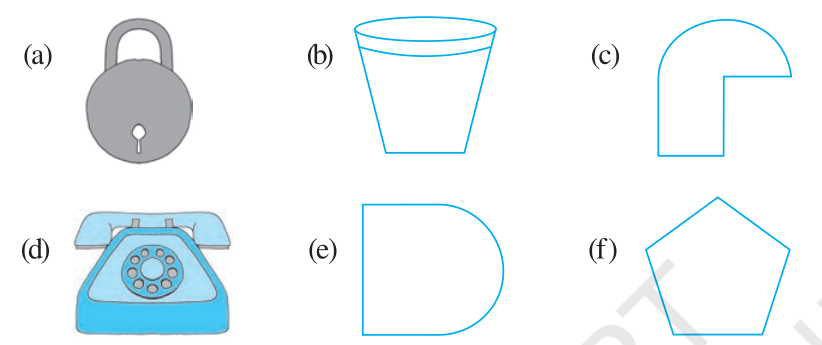
Answer
(a) Symmetric
(b) Symmetric
(c) Not Symmetric
(d) Symmetric
(e) Symmetric
(f) Symmetric
4. Copy the following on a squared paper. A square paper is what you would have used in your arithmetic notebook in earlier classes. Then complete them such that the dotted line is the line of symmetry.
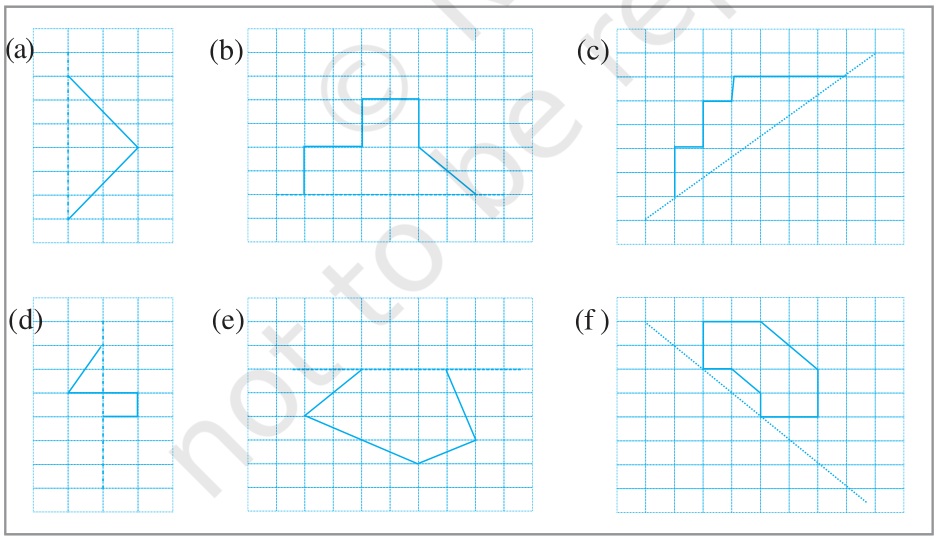

5. In the figure, l is the line of symmetry.
Complete the diagram to make it symmetric.

Answer


Answer

Exercise 13.2
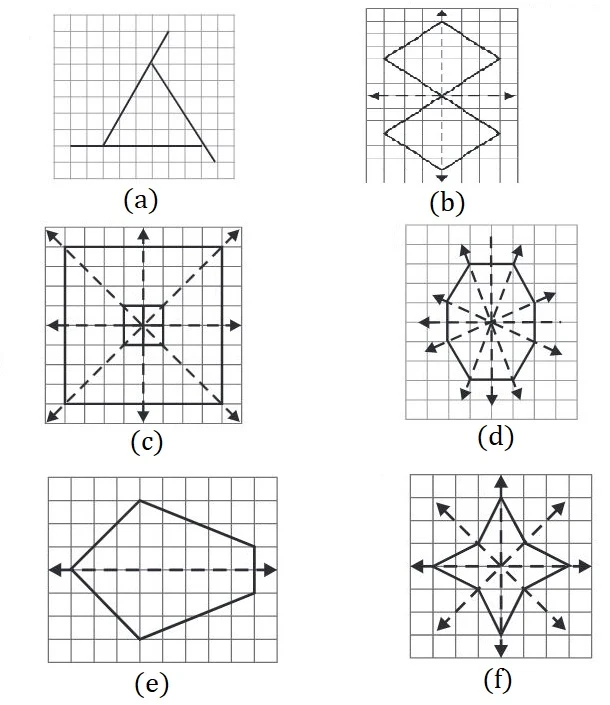
1. Find the number of lines of symmetry for each of the following shapes:

(a) 4
(b) 4
(c) 4
(d) 1
(e) 6
(f) 4
(g) 0
(h) 0
(i) 3
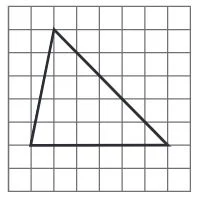
2. Copy the triangle in each of the following figures on squared paper. In each case, draw the line(s) of symmetry, if any and identify the type of triangle. (Some of you may like to trace the figures and try paper-folding first!)
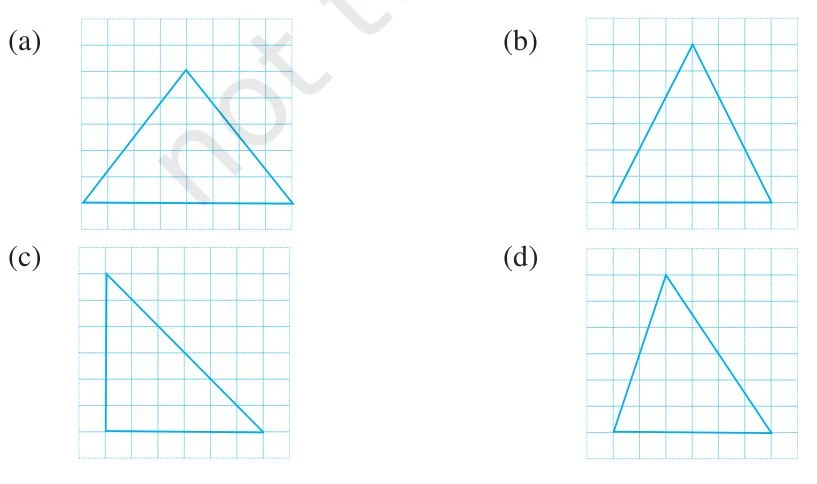
(a) l1 is the line of symmetry.
(b) l1 is the line of symmetry.
(c) l1 is the line of symmetry.
(d) No line of symmetry.
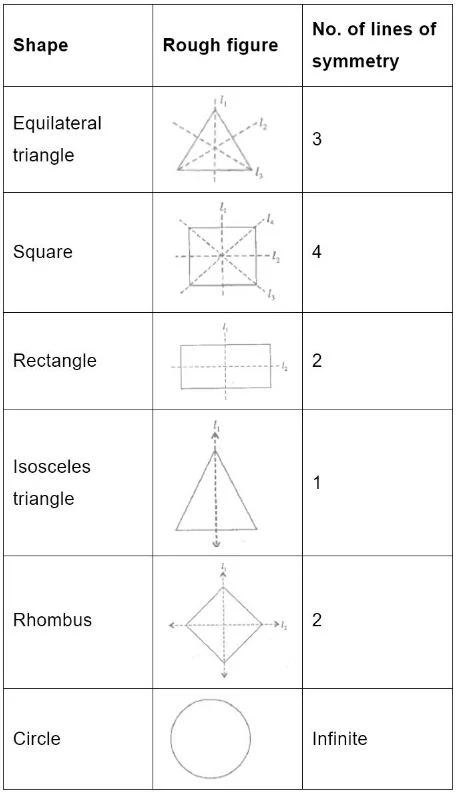
3. Complete the following table.

Answer
(a) exactly one line of symmetry?
(b) exactly two lines of symmetry?
(c) exactly three lines of symmetry?
(d) no lines of symmetry?
Sketch a rough figure in each case.
Answer
(a) Yes, Isosceles triangle
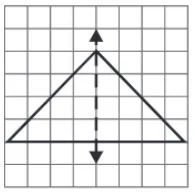
(b) No such triangle cannot be formed.
(c) Yes, Equilateral triangle.

(d) Yes, Scalene triangle
5. On a squared paper, sketch the following:
(a) A triangle with a horizontal line of symmetry but no vertical line of symmetry.
(b) A quadrilateral with both horizontal and vertical lines of symmetry.
(c) A quadrilateral with a horizontal line of symmetry but no vertical line of symmetry.
(d) A hexagon with exactly two lines of symmetry.
(e) A hexagon with six lines of symmetry.
(Hint: It will be helpful if you first draw the lines of symmetry and then complete the figures.)
Answer


6. Trace each figure and draw the lines of symmetry, if any:

Answer

(a) vertical lines of symmetry (like A)
(b) horizontal lines of symmetry (like B)
(c) no lines of symmetry (like Q)
Answer
(a) vertical lines: A, H, I, M, O, T, U, V, W, X, Y
(b) gorizontal lines: B, C, D, E, H, I, K, O, X
(c) no line of symmetry: F, G, J, N, P, Q, R, S, Z
8. Given here are figures of a few folded sheets and designs drawn about the fold. In each case, draw a rough diagram of the complete figure that would be seen when the design is cut off.

Answer

Exercise 13.3
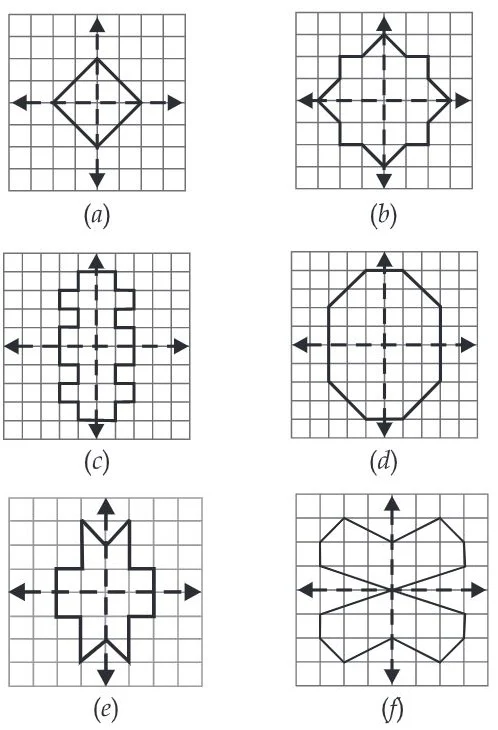
1. Find the number of lines of symmetry in each of the following shapes. How will you check your answers?

Answer
(a) four
(b) one
(c) two
(d) two
(e) one
(f) two
2. Copy the following drawing on squared paper. Complete each one of them such that the resulting figure has two dotted lines as two lines of symmetry. How did you go about completing the picture?

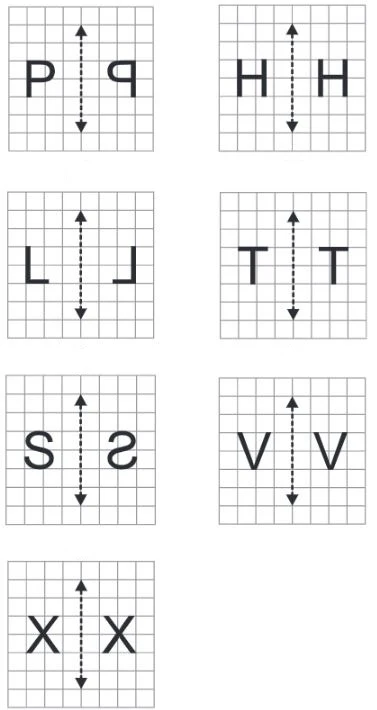
3. In each figure below, a letter of alphabet is shown along with a vertical line. Take the mirror image of the letter in the given line. Find which letters look the same after reflection (i.e., which letters look the same in the image) and which do not. Can you guess why?

Try for O E M N P H L T S V X

Chapter 13 Symmetry NCERT Solutions will prepare students to do better during immense pressure. A figure can have line symmetry if a line can be drawn dividing it into two equal halves.
• Objects that show line symmetry appear more balanced and beautiful.
• A shape may have just one or more than one lines of symmetry.
If you want solutions of a specific problem then you can find them in exercisewise NCERT Solutions of Class 6. With the help of these, you can study in an organized manner and outperform your classmates.
- Exercise 13.1 Chapter 13 Class 6 Maths NCERT Solutions
- Exercise 13.2 Chapter 13 Class 6 Maths NCERT Solutions
- Exercise 13.3 Chapter 13 Class 6 Maths NCERT Solutions
These NCERT Solutions are prepared by Studyrankers experts which will make you well versed in variety of topics and you will be able to instantly recollect your ideas and shape your answers. It help students cope with the pressure of the large examination syllabus.
NCERT Solutions for Class 6 Maths Chapters:
FAQ on Chapter 13 Symmetry
How many exercises in Chapter 13 Symmetry?
Chapter 13 contains only three exercises that are very useful in understanding the latest marking scheme and pattern of the syllabus. It will allow the students to evaluate their learning almost immediately.
How many lines of symmetry does a rectangle, a square and a parallelogram have?
Rectangle has two lines, Square has four lines and a parallelogram has no lines of symmetry.
Which letters of English alphabet have no line of symmetry?
The letters of English alphabet have no line of symmetry are F, G, J, L, N, P, Q, R, S and Z.
What do you mean by mirror line?
An object and its image are always at the same distance from the surface of a mirror, which is called the mirror line. An object and its mirror image are equal in shape and size.
