Extra Question Answer for Ch 1 Patterns in Mathematics Class 6 Maths Ganita Prakash

Extra Questions Answers for Class 6 Maths Chapter 1 Patterns in Mathematics - Ganita Prakash

Chapter 1 Patterns in Mathematics Extra Questions Answers for Class 6 Maths is provided here by studyrankers. All the questions are crafted by our experts by keeping in mind that all the important points must be covered. You can also Download PDF of Class 6 Maths Chapter 1 Patterns in Mathematics Extra Questions which will boost the student confidence and help in solving the exercises and questions from the chapter. The chapter is taken from the new NCERT Mathematics textbook, Ganita Prakash.

These Revision Notes for Class 6 Maths will develop you understanding of the chapter and help in gaining good marks in the examinations. We have also provided Chapter 1 Patterns in Mathematics NCERT Solutions which will help you in completing your homework on time. These NCERT Solutions will help an individual to increase concentration and you can solve questions of supplementary books easily. Students can also check Revision Notes for Patterns in Mathematics Class 6 Maths to prepare for their examination completely.

Important Questions for Chapter 1 Patterns in Mathematics Class 6 Maths

Question 1. Find out the missing numbers and figure out what the pattern rule is for each box.

17, 20, 23, 26, 29, __, __, __

25, 30, 35, 40, 45, __, __, __

__, __, __, 60, 70, 80, 90, 100

8, __, 24, __, 40, __, __, 64

__, __, __, 36, 45, 54, 63, 72

Answer

Question 2. Find out what type of pattern is represented by the given diagram and write number pattern for the same:

Answer

The represented pattern is cube numbers 
Number pattern is 1, 3, 27, 64,... and so on.

Question 3. Find out what type of pattern is represented by the given diagram and write number pattern for the same:

Answer

The represented pattern is of odd numbers 
Number pattern is 1, 3, 5, 7, 9, 11 ... and so on.

Question 4. What is the next number in the sequence: 1, 4, 9, 16, 25?

Answer

36
Each number in the sequence is the square of its position in the sequence (1², 2², 3², etc.), so the next number is 6² = 36.

Question 5. Find the sum of the first 10 triangular numbers.

Answer

220
Triangular numbers are formed by the formula n(n+1)/2. Adding the first 10 gives 1+3+6+10+15+21+28+36+45+55 = 220.

Question 6. If you add up the first 6 odd numbers, what square number do you get?

Answer

36

The sum of the first 6 odd numbers (1, 3, 5, 7, 9, 11) is 36, which is a square number (6²).

Question 7. Visualise the square number 64.

Answer

64 can be written as 8 × 8. Thus, it can be shown by dots as:

Question 8. Visualize cube number 1000.

Answer

1000 can be written as 10 × 10 × 10. Thus,

Question 9. What is hexagonal number? Represent it pictorially.

Answer

The numbers that can represent by a hexagon with a dot in the centre and all other dots surrounding the centre dot in a hexagonal shape.
For example: 1, 7, 19, 37, 61, 91, ……

Pictorial representation:

Question 10. Represent first 7 centered hexagonal numbers pictorially.

Answer

The first six centered hexagonal numbers are as follows: 1, 7, 19, 37, 61, 91, 127.

Pictorial representation:

Question 10. Which of the following is not a sequence of powers?

(i) 1, 2, 4, 8, 16
(ii) 1, 3, 9, 27, 81
(iii) 1, 5, 25, 125, 625
(iv) 1, 3, 6, 10, 15

Answer

(iv) 1, 3, 6, 10, 15

This sequence represents triangular numbers, not powers, where each term represents a triangular shape formed by dots.

Question 11. Complete the following number sequences:

(a) 1 + 3 + 5 + ___ + 9 + 11 = ____.
(b) 1 + ___ + 3 + 4 + 3 + 2 + 1 = ____.
(c) 1 + 2 + 3 + __ + 5 + __ + 7 +…..+ 11 + __+ …. + 7 + ___ + 5 + 4 + 3 + 2 + 1 = 121 

Answer

(a) 1 + 3 + 5 + 7 + 9 + 11 = 36.

(b) 1 + 2 + 3 + 4 + 3 + 2 + 1 = 16.

(c) 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 121

Question 12. Identify the patterns and write the next three numbers to complete the given patterns.

(a) 1, 3, 6, 10, 15, ….., …., ….
(b) 1, 4, 9, 16, 25, …, …, ….
(c) 1, 8, 27, 64, 125, …, …, ….

Answer

(a) The given pattern is as follows:
1, 1 + 2 = 3, 1 + 2 + 3 = 6, 1 + 2 + 3 + 4 = 10, 1 + 2 + 3 + 4 + 5 = 15; a pattern of triangular numbers. Therefore, the next three numbers of this pattern are:
1 + 2 + 3 + 4 + 5 + 6 = 21,
1 + 2 + 3 + 4 + 5 + 6 + 7 = 28,
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36.

(b) The given pattern is as follows:
1 × 1 = 1, 2 × 2 = 4, 3 × 3 = 9, 4 × 4 = 16, 5 × 5 = 25; a pattern of square numbers.
Therefore, the next three numbers of this pattern are: 6 × 6 = 36, 7 × 7 = 49, 8 × 8 = 64.

(c) The given pattern is as follows:
1 × 1 × 1 = 1, 2 × 2 × 2 = 8, 3 × 3 × 3 = 27, 4 × 4 × 4 = 64, 5 × 5 × 5 = 125; a pattern of cubes.
Therefore, the next three numbers of this pattern are: 6 × 6 × 6 = 216, 7 × 7 × 7 = 343, 8 × 8 × 8 = 512.

Fill in the Blanks

Question 1. A ______ polygon is a shape with all sides and angles equal.

Answer

regular

 The term "regular" in geometry means that all sides and angles of the polygon are equal.

Question 2. The sequence 1, 8, 27, 64, ... represents the ______ of numbers.

Answer

cubes

These numbers are the cubes of the natural numbers: 1³,2³,3³,4³, 5³, 6³, ....

Question 3. ______ numbers can be represented as dots forming a perfect square.

Answer

Square

Square numbers can be visualized by arranging dots in a grid where the number of rows equals the number of columns.

Question 4. The pattern 2, 4, 6, 8, 10, ... is a sequence of _____ numbers.

Answer

even

This sequence is formed by adding 2 to the previous number, which creates a sequence of even numbers.

Question 5. Continue the pattern for the next three terms: 1, 2, 4, 8, ___ , ___ , ___.

Answer

16, 32, 64

Each term is double the previous term, thus continuing: 8×2 = 16, 16×2 = 32, 32×2 = 64.

Question 6. ______ numbers increase by the same amount each time, and this sequence is called counting numbers.

Answer

Natural

The natural or counting numbers increase by 1 each time: 1, 2, 3, 4, ...

True or False

Question 1. The sequence 1, 4, 9, 16, 25, ... is an example of cube numbers.

Answer

False

This sequence is an example of square numbers, not cube numbers.

Question 2. A regular pentagon has equal sides but different angles.

Answer

False

A regular pentagon has both equal sides and equal angles.

Question 3. The sequence of odd numbers starts with 1, 3, 5, 7, ...

Answer

True

The odd number sequence starts with 1 and increases by 2 each time.

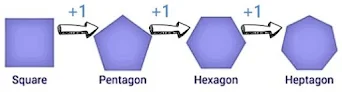
Question 4. A shape sequence starting with a square and adding one side each time would form polygons with increasing numbers of sides.

Answer

True

This sequence would start with a square (4 sides), then a pentagon (5 sides), and so on, each with one more side.

Question 5. The number 36 can be both a square number and a triangular number.

Answer

True

The number 36 is unique in that it can be represented both as a square number (6x6) and as a triangular number.

​Word Problem

Question 1. Riya is stacking books in a pyramid shape. The first row has 1 book, the second has 3, the third has 6. If she continues this pattern, how many books will be in the fifth row?

Answer

The books in each row follow a pattern:

• 1st row: 1
• 2nd row: 1 + 2 = 3
• 3rd row: 1 + 2 + 3 = 6
• 4th row: 1 + 2 + 3 + 4 = 10
• 5th row: 1 + 2 + 3 + 4 + 5 = 15

The fifth row will have 15 books.

Question 2. A honeycomb follows a hexagonal pattern. If the first row has 1 cell, the second has 7 cells, and the third has 19 cells, how many will be in the fourth row? 

Answer

The number of cells follows this pattern:

• 1st row = 1
• 2nd row = 1 + 6 = 7
• 3rd row = 7 + 12 = 19
• 4th row = 19 + 18 = 37

The fourth row will have 37 cells.

Question 3. A school’s staircase follows a pattern: The first step has 2 tiles, the second has 4, the third has 6. How many tiles will be on the 10th step?

Answer

Each step increases by 2 tiles. The sequence follows:

• 1st step = 2
• 2nd step = 4
• 3rd step = 6
• 4th step = 8
• …
• 10th step = 2 × 10 = 20

The 10th step will have 20 tiles.

Question 4. Give a diagrammatic representation of triangular numbers.

Answer

Question 5. Represent 36 as both triangular and square numbers.

Answer

(i) 36 as triangular number

(ii) 36 as square number 

Assertion Reason

In the given question, a statement of Assertion is followed by a statement of Reason. Choose the correct option as:

(a) Both assertion and reason arp true and the reason is the correct explanation of assertion.
(b) Both assertion and reason are true but the reason is not the correct explanation of the assertion.
(c) Assertion is true and the reason is false.
(d) Assertion is false and the reason is true.

(i) Assertion: 15 is both a triangular number and a square number. 

Reason: If dots arrangement of a number is represented in triangle as well as in square, then the number is called both triangular as well as square number or square- triangular number.

Answer

(d) Since, 15 dots can be arranged in a triangle, but cannot be arranged in a square.

(ii) Given the sequence 1, 3, 6, 10, 15, find the sum of the next two terms. 

Answer

56 (21 + 28)

Continuing the sequence of triangular numbers: 6(6+1)/2 = 21, 7(7+1)/2 = 28. The sum is 21+28 = 49.

Case Based Question

Rima and Diva are playing with square counters.
Rima arranges her counters as follows:

Diva arranges the counters as follows:

One of their friends, Rohan, says these are showing the number patterns.
Based on the above information, answer the following questions.

(a) What are the number patterns they are showing?

(b) If Rima’s arrangement is representing the triangular numbers, then what will be her next two arrangements if she follows the same pattern?

(c) What is Diva’s next arrangement with counters if she follows the same pattern?

Answer

(a) The number pattern represented by Rima’s arrangement is: 1, 3, 6, …, which are triangular numbers.
Diva’s arrangement represents the pattern: 1,4,9,…, which are square numbers.

(b) The next triangular numbers are 10 and 15. So, Rima’s arrangement for these triangular numbers is as follows:

(c) The next square number is 16. So, Diva’s arrangement for the number 16 is as follows: