NCERT Solutions for Class 7 Maths Chapter 14 Symmetry| PDF Download
On this page you will get Chapter 14 Symmetry NCERT Solutions for Class 7 Maths which is very useful during the preparation of examinations and encourage students to learn new topics. You can download PDF of Chapter 13 Exponents and Powers NCERT Solutions which give good experience and provide opportunities to learn new things. It is very challenging to score good marks in tests that is why we have prepared NCERT Solutions.
Class 7 NCERT Solutions will help you in analyzing the problems and answering it with precision and the right concepts. These NCERT Solutions help you in analyzing the problems and answering it with precision and the right concepts.

Exercise 14.1
1. Copy the figures with punched holes and find the axes of symmetry for the following:
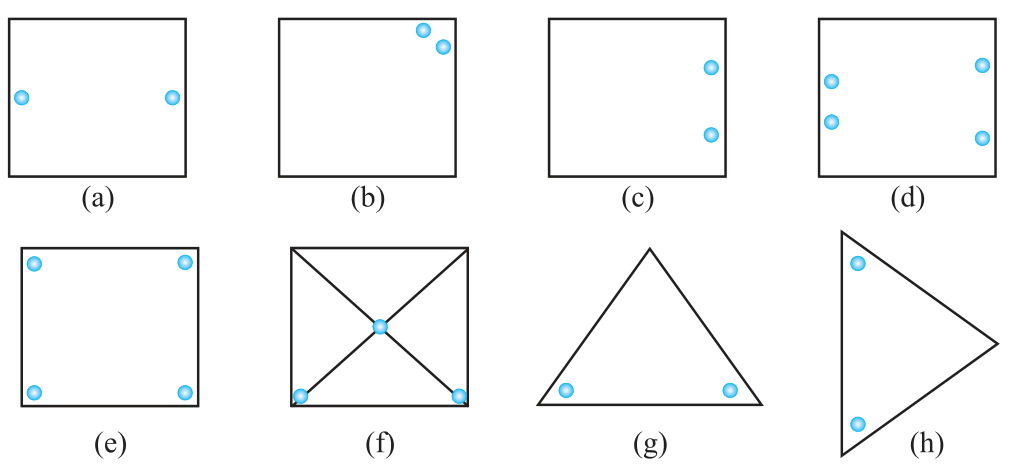

Answer



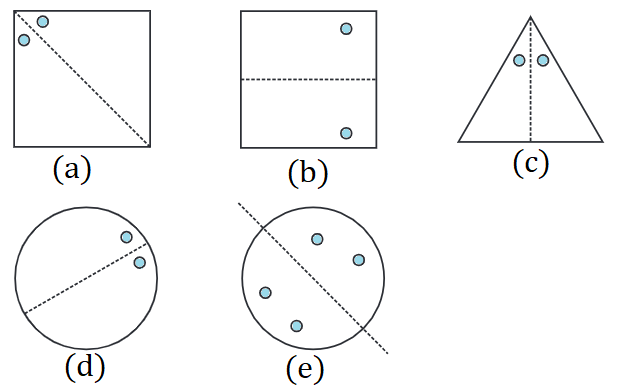
3. In the following figures, the mirror line (i.e., the line of symmetry) is given as a dotted line. Complete each figure performing reflection in the dotted (mirror) line. (You might perhaps place a mirror along the dotted line and look into the mirror for the image). Are you able to recall the name of the figure you complete?

Answer
(a) Square
(b) Triangle
(c) Rhombus
(d) Circle
(e) Pentagon
(f) Hexagon

4. The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry.


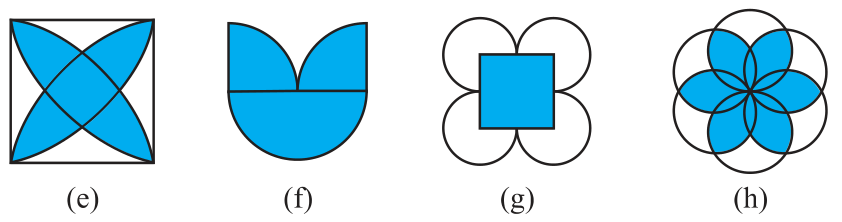
Answer

Take any one diagonal as a line of symmetry and shade a few more squares to make the figure symmetric about a diagonal. Is there more than one way to do that? Will the figure be symmetric about both the diagonals?



Answer

Yes, there is more than one way and this figure will be symmetric about both the diagonals.
6. Copy the diagram and complete each shape to be symmetric about the mirror line(s):

Answer

(a) An equilateral triangle
(b) An isosceles triangle
(c) A scalene triangle
(d) A square
(e) A rectangle
(f) A rhombus
(g) A parallelogram
(h) A quadrilateral
(i) A regular hexagon
(j) A circle
Answer
(a) An equilateral triangle - Three Lines
(b) An isosceles triangle - Only One Line
(c) A scalene triangle - No Line
(d) A square - Four Lines
(e) A rectangle - Two Lines
(f) A rhombus - Four Lines
(g) A parallelogram - No Line
(h) A quadrilateral - No Line
(i) A regular hexagon - Six Lines
(j) A circle - Infinite Lines
8. What letters of the English alphabet have reflectional symmetry (i.e., symmetry related to mirror reflection) about.
(a) a vertical mirror
(b) a horizontal mirror
(c) both horizontal and vertical mirrors
Answer
(a) Vertical mirror - A, H, I, M, 0, T, U, V, W, X and Y
(b) Horizontal mirror - B, C, D, E, H, I, 0 and X
(c) both horizontal and vertical mirrors - O, X,I, H
9. Give three examples of shapes with no line of symmetry.
Answer
The three examples are:
1. Quadrilateral
2. Scalene triangle
3. Parallelogram
10. What other name can you give to the line of symmetry of
(a) an isosceles triangle? (b) a circle?
Answer
(a) The line of symmetry of an isosceles triangle is median or altitude.
(b) The line of symmetry of a circle is diameter.
Exercise 14.2
1. Which of the following figures have rotational symmetry of order more than 1:

Rotational symmetry of order more than 1 are (a),(b),(d),(e) and (f).
2. Give the order the rotational symmetry for each figure:

Answer
(a) 2
(b) 2
(c) 3
(d) 4
(e) 4
(f) 5
(g) 6
(h) 3
Exercise 14.3
1. Name any two figures that have both line symmetry and rotational symmetry.
Answer
Circle and Equilateral Triangle.
2. Draw, wherever possible, a rough sketch of:
(i) a triangle with both line and rotational symmetries of order more than 1.
(ii) a triangle with only line symmetry and no rotational symmetry of order more than 1.
(iii) a quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
(iv) a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
Answer
(i) An equilateral triangle has both line and rotational symmetries of order more than 1.
(ii) An isosceles triangle has only one line of symmetry and no rotational symmetry of order more than 1.
(iii) It is not possible because order of rotational symmetry is more than 1 of a figure, most acertain the line of symmetry.
(iv) A trapezium which has equal non-parallel sides, a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
3. In a figure has two or more lines of symmetry, should it have rotational symmetry of order more than 1?
Answer
Yes, because every line through the centre forms a line of symmetry and it has rotational symmetry around the centre for every angle.
4. Fill in the blanks:
| Shape | Centre of Rotation | Order of Rotation | Angle of Rotation |
| Square | - | - | - |
| Rectangle | - | - | - |
| Rhombus | - | - | - |
| Equilateral triangle | - | - | - |
| Regular hexagon | - | - | - |
| Circle | - | - | - |
| Semi-circle | - | - | - |
Answer
| Shape | Centre of Rotation | Order of Rotation | Angle of Rotation |
| Square | Intersecting point of diagonals. | 4 | 90° |
| Rectangle | Intersecting point of diagonals. | 2 | 180° |
| Rhombus | Intersecting point of diagonals. | 2 | 180° |
| Equilateral triangle | Intersecting point of medians. | 3 | 120° |
| Regular hexagon | Intersecting point of diagonals. | 6 | 60° |
| Circle | Centre | Infinite | At every point |
| Semi-circle | Mid-point of diameter | 1 | 360° |
5. Name the quadrilaterals which have both line and rotational symmetry of order more than 1.
Answer
Square has both line and rotational symmetry of order more than 1.
6. After rotating by 60° about a centre, a figure looks exactly the same as its original position. At what other angles will this happen for the figure?
Answer
After rotating by 60° about a centre, a figure looks exactly the same as its original position. This will happen for the figure at angles 120°, 180°, 240°, 300°, 360° respectively.
7. Can we have a rotational symmetry whose angle of rotation is
(i) 45°?
(ii) 17°?
Answer
(i) Yes
(ii) No.
Go Back To NCERT Solutions for Class 7 Maths
NCERT Solutions for Class 7 Maths Chapter 14 Symmetry
Chapter 14 NCERT Solutions will help you in completing homework on time. The word symmetry comes from the Greek word symmetros, which means even. A figure has line symmetry if a line can be drawn dividing it into two identical parts. The line is called the line of symmetry or axis of symmetry. Any object or shape is said to have rotational symmetry if it looks exactly the same at least once during a complete rotation through three hundred and sixty degrees.
If you want exercisewise Class 7 Maths NCERT Solutions then you can find them which will help you in finding specific question that you're looking for. Through the help of these NCERT Solutions, you can figure out the latest marking scheme and develop your own strategy to tackle questions.
- Exercise 14.1 Chapter 14 Class 7 Maths NCERT Solutions
- Exercise 14.2 Chapter 14 Class 7 Maths NCERT Solutions
- Exercise 14.3 Chapter 14 Class 7 Maths NCERT Solutions
Class 7 NCERT Solutions prepared by Subject matter experts of Studyrankers will help you in analyzing the problems and answering it with precision and the right concepts. will help you in understanding the important concepts of the chapter properly and increase concentration among students.
NCERT Solutions for Class 7 Maths Chapters:
FAQ on Chapter 14 Symmetry
How many exercises are there in Chapter 14 Symmetry Class 7 Maths NCERT Solutions?
There are three exercises in the Chapter 14 that will develop your understandings of the chapter and make you able to solve more questions. These NCERT Solutions will be helpful in gaining good marks in the exams and make student confident.
What is the order of rotational symmetry of a circle?
Centre of rotation.
What is the Centre of rotation of an equilateral triangle?
Centroid is the centre of rotation of an equilateral triangle.
Which figure has neither a line of symmetry non a rotational symmetry?
Quadrilateral has neither a line of symmetry non a rotational symmetry.
