NCERT Solutions for Class 10 Maths Chapter Constructions (Removed from Syllabus)
We have provided NCERT Solutions for Class 10 Maths Ch 11 Constructions in this page which will be helpful in completing your homework in less time. It will encourage students to learn new topics and give better understanding of the chapter. Class 10 NCERT Solutions is the best way to revise whole chapter properly and learning efficiently. These solutions are updated according to the latest pattern of CBSE.
Exercise 11.1
In each of the following, give the justification of the construction also:
1. Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.
Answer
Step I: AB = 7.6 cm is drawn.
Step II: A ray AX making an acute angle with AB is drawn.
Step III: After that, a ray BY is drawn parallel to AX making equal acute angle as in the previous step.
Step IV: Point A1, A2, A3, A4 and A5 is marked on AX and point B1, B2.... to B8 is marked on BY such that AA1 = A1A2 = A2A3 =....BB1= B1B2 = .... B7B8
Step V: A5 and B8 is joined and it intersected AB at point C diving it in the ratio 5:8.
AC : CB = 5 : 8
Justification:
ΔAA5C ~ ΔBB8C
∴ AA5/BB8 = AC/BC = 5/8
2. Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are 2/3 of the corresponding sides of the first triangle.
Answer
Steps of Construction:
Step I: AB = 6 cm is drawn.Step II: With A as a centre and radius equal to 4 cm, an arc is draw.
Step III: Again, with B as a centre and radius equal to 5 cm an arc is drawn on same side of AB intersecting previous arc at C.
Step IV: AC and BC are joined to form ΔABC.
Step V: A ray AX is drawn making an acute angle with AB below it.
Step VI: 5 equal points (sum of the ratio = 2 + 3 =5) is marked on AX as A1 A2....A5
Step VII: A5B is joined. A2B' is drawn parallel to A5B and B'C' is drawn parallel to BC.
ΔAB'C' is the required triangle
Justification:
∠A(Common)
∠C = ∠C' and ∠B = ∠ B' (corresponding angles)
Thus ΔAB'C' ~ ΔABC by AAA similarity condition
From the figure,
AB'/AB = AA2/AA5 = 2/3
AB' =2/3 AB
AC' = 2/3 AC
3. Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are
7/5 of the corresponding sides of the first triangle.
Answer
Steps of Construction:
Step I: A triangle ABC with sides 5 cm, 6 cm and 7 cm is drawn.
Step II: A ray BX making an acute angle with BC is drawn opposite to vertex A.Step III: 7 points as B1 B2 B3 B4 B5 B6 and B7 are marked on BX.
Step IV; Point B5 is joined with C to draw B5C.
Step V: B7C' is drawn parallel to B5C and C'A' is parallel to CA.
Thus A'BC' is the required triangle.
Justification
ΔAB'C' ~ ΔABC by AAA similarity condition
∴ AB/A'B = AC/A'C' = BC/BC'
and BC/BC' = BB5/BB7 = 5/7
∴A'B/AB = A'C'/AC = = BC'/BC = 7/5
4. Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 1.5 times the corresponding sides of the isosceles triangle.
Answer
Steps of Construction:
Step I: BC = 5 cm is drawn.Step II: Perpendicular bisector of BC is drawn and it intersect BC at O.
Step III: At a distance of 4 cm, a point A is marked on perpendicular bisector of BC.
Step IV: AB and AC is joined to form ΔABC.
Step V: A ray BX is drawn making an acute angle with BC opposite to vertex A.
Step VI: 3 points B1 B2 and B3 is marked BX.
Step VII: B2 is joined with C to form B2C.
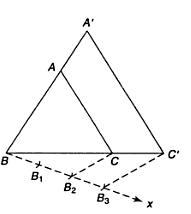Step VIII: B3C' is drawn parallel to B2C and C'A' is drawn parallel to CA.Thus, A'BC' is the required triangle formed.
Justification:
ΔAB'C' ~ ΔABC by AA similarity condition.
∴ AB/AB' = BC/B'C' = AC/AC'
also,
AB/AB' = AA2/AA3 = 2/3
⇒ AB' = 3/2 AB, B'C' = 3/2 BC and AC' = 3/2 AC
5. Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are 3/4 of the corresponding sides of the triangle ABC.
Answer
Steps of Construction:
Step I: BC = 6 cm is drawn.
Step II: At point B, AB = 5 cm is drawn making an
∠ABC = 60° with BC.
Step III: AC is joined to form ΔABC.
Step IV: A ray BX is drawn making an acute angle with BC opposite to vertex A.
Step V: 4 points B1 B2 B3 and B4 at equal distance is marked on BX.
Step VII: B3 is joined with C' to form B3C'.
Step VIII: C'A' is drawn parallel CA.
Thus, A'BC' is the required triangle.
Justification:
∠A = 60° (Common)
∠C = ∠C'
ΔAB'C' ~ ΔABC by AA similarity condition.
∴ AB/AB' = BC/B'C' = AC/AC'
also,
AB/AB' = AA3/AA4 = 4/3
⇒ AB' = 3/4 AB, B'C' = 3/4 BC and AC' = 3/4 AC
6. Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are 4/3 times the corresponding sides of Δ ABC.
Answer
Sum of all side of triangle = 180°
∴ ∠A + ∠B + ∠C = 180°
∠C = 180° - 150° = 30°
Steps of Construction:
Step I: BC = 7 cm is drawn.
Step II: At B, a ray is drawn making an angle of 45° with BC.
Step III: At C, a ray making an angle of 30° with BC is drawn intersecting the previous ray at A. Thus, ∠A = 105°.
Step IV: A ray BX is drawn making an acute angle with BC opposite to vertex A.
Step V: 4 points B1 B2 B3 and B4 at equal distance is marked on BX.
Step VI: B3C is joined and B4C' is made parallel to B3C.
Step VII: C'A' is made parallel CA.
Thus, A'BC' is the required triangle.
Justification:
∠B = 45° (Common)
∠C = ∠C'
ΔAB'C' ~ ΔABC by AA similarity condition.
∴ BC/BC' = AB/A'B' = AC/A'C'
also,
BC/BC' = BB3/BB4 = 34
⇒ AB = 4/3 AB', BC = 4/3 BC' and AC = 4/3 A'C'
7. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle.
Answer
Steps of Construction:
Step I: BC = 3 cm is drawn.
Step II: At B, A ray making an angle of 90° with BC is drawn.
Step III: With B as centre and radius equal to 4 cm, an arc is made on previous ray intersecting it at point A.
Step IV: AC is joined to form ΔABC.
Step V: A ray BX is drawn making an acute angle with BC opposite to vertex A.
Step VI: 5 points B1 B2 B3 B4 and B5 at equal distance is marked on BX.
Step VII: B3C is joined B5C' is made parallel to B3C.
Step VIII: A'C' is joined together.
Thus, ΔA'BC' is the required triangle.
Justification:
As in the previous question 6.
Page No. 221
Exercise 11.2
In each of the following, give also the justification of the construction:
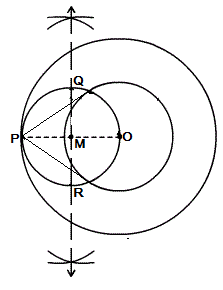
1. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Answer
Steps of Construction:
Step I: With O as a centre and radius equal to 6 cm, a circle is drawn.
Step II: A point P at a distance of 10 cm from the centre O is taken. OP is joined.
Step III: Perpendicular bisector OP is drawn and let it intersected at M.
Step IV: With M as a centre and OM as a radius, a circle is drawn intersecting previous circle at Q and R.
Step V: PQ and PR are joined.
Thus, PQ and PR are the tangents to the circle.
On measuring the length, tangents are equal to 8 cm.
PQ = PR = 8cm.
Justification:
OQ is joined.
∠PQO = 90° (Angle in the semi circle)
∴ OQ ⊥ PQ
Therefor, OQ is the radius of the circle then PQ has to be a tangent of the circle.
Step II: At point B, AB = 5 cm is drawn making an
∠ABC = 60° with BC.
Step III: AC is joined to form ΔABC.
Step IV: A ray BX is drawn making an acute angle with BC opposite to vertex A.
Step V: 4 points B1 B2 B3 and B4 at equal distance is marked on BX.
Step VII: B3 is joined with C' to form B3C'.
Step VIII: C'A' is drawn parallel CA.
Thus, A'BC' is the required triangle.
Justification:
∠A = 60° (Common)
∠C = ∠C'
ΔAB'C' ~ ΔABC by AA similarity condition.
∴ AB/AB' = BC/B'C' = AC/AC'
also,
AB/AB' = AA3/AA4 = 4/3
⇒ AB' = 3/4 AB, B'C' = 3/4 BC and AC' = 3/4 AC
6. Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are 4/3 times the corresponding sides of Δ ABC.
Answer
Sum of all side of triangle = 180°
∴ ∠A + ∠B + ∠C = 180°
∠C = 180° - 150° = 30°
Steps of Construction:
Step I: BC = 7 cm is drawn.
Step II: At B, a ray is drawn making an angle of 45° with BC.
Step III: At C, a ray making an angle of 30° with BC is drawn intersecting the previous ray at A. Thus, ∠A = 105°.Step IV: A ray BX is drawn making an acute angle with BC opposite to vertex A.
Step V: 4 points B1 B2 B3 and B4 at equal distance is marked on BX.
Step VI: B3C is joined and B4C' is made parallel to B3C.
Step VII: C'A' is made parallel CA.
Thus, A'BC' is the required triangle.
Justification:
∠B = 45° (Common)
∠C = ∠C'
ΔAB'C' ~ ΔABC by AA similarity condition.
∴ BC/BC' = AB/A'B' = AC/A'C'
also,
BC/BC' = BB3/BB4 = 34
⇒ AB = 4/3 AB', BC = 4/3 BC' and AC = 4/3 A'C'
7. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle.
Answer
Step I: BC = 3 cm is drawn.
Step II: At B, A ray making an angle of 90° with BC is drawn.
Step III: With B as centre and radius equal to 4 cm, an arc is made on previous ray intersecting it at point A.
Step IV: AC is joined to form ΔABC.
Step V: A ray BX is drawn making an acute angle with BC opposite to vertex A.
Step VI: 5 points B1 B2 B3 B4 and B5 at equal distance is marked on BX.
Step VII: B3C is joined B5C' is made parallel to B3C.
Step VIII: A'C' is joined together.
Thus, ΔA'BC' is the required triangle.
Justification:
As in the previous question 6.
Page No. 221
Exercise 11.2
In each of the following, give also the justification of the construction:
1. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Answer
Step I: With O as a centre and radius equal to 6 cm, a circle is drawn.
Step II: A point P at a distance of 10 cm from the centre O is taken. OP is joined.
Step III: Perpendicular bisector OP is drawn and let it intersected at M.
Step IV: With M as a centre and OM as a radius, a circle is drawn intersecting previous circle at Q and R.
Step V: PQ and PR are joined.
Thus, PQ and PR are the tangents to the circle.
On measuring the length, tangents are equal to 8 cm.
PQ = PR = 8cm.
Justification:
OQ is joined.
∠PQO = 90° (Angle in the semi circle)
∴ OQ ⊥ PQ
Therefor, OQ is the radius of the circle then PQ has to be a tangent of the circle.
Similarly, PR is a tangent of the circle.
2. Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Answer
Steps of Construction:
Step I: With O as a centre and radius equal to 4 cm, a circle is drawn.
Step II: With O as a centre and radius equal to 6 cm, a concentric circle is drawn.
Step III: P be any point on the circle of radius 6 cm and OP is joined.
Step IV: Perpendicular bisector of OP is drawn which cuts it at M
Step V: With M as a centre and OM as a radius, a circle is drawn which intersect the the circle of radius 4 cm at Q and R
Step VI: PQ and PR are joined.
Thus, PQ and PR are the two tangents.
Measurement:
OQ = 4 cm (Radius of the circle)
PQ = 6 cm ( Radius of the circle)
∠PQO = 90° (Angle in the semi circle)
Applying Pythagoras theorem in ΔPQO,
PQ2 + QO2 = PO2⇒ PQ2 + 42= 62
⇒ PQ2 + 16 = 36
⇒ PQ2 = 36 - 16
⇒ PQ2 = 20
⇒ PQ = 2√5
Justification:
∠PQO = 90° (Angle in the semi circle)
⇒ PQ2 = 36 - 16
⇒ PQ2 = 20
⇒ PQ = 2√5
Justification:
∠PQO = 90° (Angle in the semi circle)
∴ OQ ⊥ PQ
Therefor, OQ is the radius of the circle then PQ has to be a tangent of the circle.
Therefor, OQ is the radius of the circle then PQ has to be a tangent of the circle.
Similarly, PR is a tangent of the circle.
3. Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Answer
Steps of Construction:
Step I: With O as a centre and radius equal to 3 cm, a circle is drawn.
Step II: The diameter of the circle is extended both sides and an arc is made to cut it at 7 cm.
Step III: Perpendicular bisector of OP and OQ is drawn and x and y be its mid-point.
Step IV: With O as a centre and Ox be its radius, a circle is drawn which intersected the previous circle at M and N.
Step V: Step IV is repeated with O as centre and Oy as radius and it intersected the circle at R and T.
Step VI: PM and PN are joined also QR and QT are joined.
Thus, PM and PN are tangents to the circle from P and QR and QT are tangents to the circle from point Q.
Justification:
∠PMO = 90° (Angle in the semi circle)
3. Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Answer
Step I: With O as a centre and radius equal to 3 cm, a circle is drawn.
Step II: The diameter of the circle is extended both sides and an arc is made to cut it at 7 cm.
Step III: Perpendicular bisector of OP and OQ is drawn and x and y be its mid-point.
Step IV: With O as a centre and Ox be its radius, a circle is drawn which intersected the previous circle at M and N.
Step V: Step IV is repeated with O as centre and Oy as radius and it intersected the circle at R and T.
Step VI: PM and PN are joined also QR and QT are joined.
Thus, PM and PN are tangents to the circle from P and QR and QT are tangents to the circle from point Q.
Justification:
∠PMO = 90° (Angle in the semi circle)
∴ OM ⊥ PM
Therefor, OM is the radius of the circle then PM has to be a tangent of the circle.
Therefor, OM is the radius of the circle then PM has to be a tangent of the circle.
Similarly, PN, QR and QT are tangents of the circle.
4. Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Answer
We know that radius of the circle is perpendicular to the tangents.
Sum of all the 4 angles of quadrilateral = 360°
∴ Angle between the radius (∠O) = 360° - (90° + 90° + 60°) = 120°
Steps of Construction:
Step I: A point Q is taken on the circumference of the circle and OQ is joined. OQ is radius of the circle.
Step II: Draw another radius OR making an angle equal to 120° with the previous one.
Step III: A point P is taken outside the circle. QP and PR are joined which is perpendicular OQ and OR.
Thus, QP and PR are the required tangents inclined to each other at an angle of 60°.
Justification:
Sum of all angles in the quadrilateral PQOR = 360°
∠QOR + ∠ORP + ∠OQR + ∠RPQ = 360°
⇒ 120° + 90° + 90° + ∠RPQ = 360°
⇒∠RPQ = 360° - 300°
⇒∠RPQ = 60°
Hence, QP and PR are tangents inclined to each other at an angle of 60°.
5. Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Answer
Steps of Construction:
Step I: A line segment AB of 8 cm is drawn.
Step II: With A as centre and radius equal to 4 cm, a circle is drawn which cut the line at point O.
Step III: With B as a centre and radius equal to 3 cm, a circle is drawn.
Step IV: With O as a centre and OA as a radius, a circle is drawn which intersect the previous two circles at P, Q and R, S.
Step V: AP, AQ, BR and BS are joined.
Thus, AP, AQ, BR and BS are the required tangents.
Justification:
∠BPA = 90° (Angle in the semi circle)
Step IV: OA is joined and a circle is drawn with diameter OA which intersected the previous circle at B and E.
Step V: AE is joined.
Thus, AB and AE are the required tangents to the circle from A.
Justification:
∠OEA = 90° (Angle in the semi circle)
4. Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Answer
Sum of all the 4 angles of quadrilateral = 360°
∴ Angle between the radius (∠O) = 360° - (90° + 90° + 60°) = 120°
Steps of Construction:
Step I: A point Q is taken on the circumference of the circle and OQ is joined. OQ is radius of the circle.
Step II: Draw another radius OR making an angle equal to 120° with the previous one.
Step III: A point P is taken outside the circle. QP and PR are joined which is perpendicular OQ and OR.
Thus, QP and PR are the required tangents inclined to each other at an angle of 60°.
Justification:
Sum of all angles in the quadrilateral PQOR = 360°
∠QOR + ∠ORP + ∠OQR + ∠RPQ = 360°
⇒ 120° + 90° + 90° + ∠RPQ = 360°
⇒∠RPQ = 360° - 300°
⇒∠RPQ = 60°
Hence, QP and PR are tangents inclined to each other at an angle of 60°.
5. Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Answer
Step I: A line segment AB of 8 cm is drawn.
Step II: With A as centre and radius equal to 4 cm, a circle is drawn which cut the line at point O.
Step III: With B as a centre and radius equal to 3 cm, a circle is drawn.
Step IV: With O as a centre and OA as a radius, a circle is drawn which intersect the previous two circles at P, Q and R, S.
Step V: AP, AQ, BR and BS are joined.
Thus, AP, AQ, BR and BS are the required tangents.
Justification:
∠BPA = 90° (Angle in the semi circle)
∴ AP ⊥ PB
Therefor, BP is the radius of the circle then AP has to be a tangent of the circle.
Therefor, BP is the radius of the circle then AP has to be a tangent of the circle.
Similarly, AQ, BR and BS are tangents of the circle.
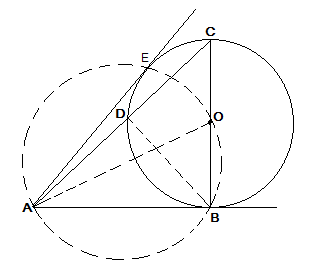
6. Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Answer
Steps of Construction:
Step I: A ΔABC is drawn.
Step II: Perpendicular to AC is drawn to point B which intersected it at D.
Step III: With O as a centre and OC as a radius, a circle is drawn. The circle through B, C, D is drawn.6. Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Answer
Step I: A ΔABC is drawn.
Step II: Perpendicular to AC is drawn to point B which intersected it at D.
Step IV: OA is joined and a circle is drawn with diameter OA which intersected the previous circle at B and E.
Step V: AE is joined.
Thus, AB and AE are the required tangents to the circle from A.
Justification:
∠OEA = 90° (Angle in the semi circle)
∴ OE ⊥ AE
Therefor, OE is the radius of the circle then AE has to be a tangent of the circle.
Therefor, OE is the radius of the circle then AE has to be a tangent of the circle.
NCERT Solutions for Class 10 Maths Chapter 11 Constructions
Class 11 Constructions NCERT Solutions will be very useful in preparation of the examinations and understanding the concepts properly. There are three exercises given in Chapter 11 Constructions which will embed with you knowledge about various types of mathematical constructions.
• Introduction: In earlier class, we have done certain constructions such as bisecting an angle, drawing the perpendicular bisector of a line segment, some constructions of triangles etc. and in this chapter, we will be doing more constructions like that and will give mathematical reasoning behind them.
• Division of a Line Segment: We will be dividing a line segment in a given ratio and construct a triangle similar to a given triangle as per given scale factor.
• Construction of Tangents to a Circle: We have to construct the tangents to a circle from a point outside it and provide justification of the construction also.
If you want to access other Study material for Class 10 then you can find them below.
There are only two exercises in the Chapter 11 Constructions which will improve your logical and thinking skills. We have also provided NCERT Solutions for Class 10 Maths exercisewise which you can get from below.
NCERT Solutions for Class 10 Maths Chapters:
FAQ on Chapter 11 Constructions
How many exercises in Chapter 11 Constructions
There are 2 exercise in the Chapter 11 Constructions Class 10 Maths which are prepared by Studyrankers which will give in depth learning about the concepts.
If a point lies inside a circle, then there cannot be a ______ to the circle through this point.
Tangent
What is Scale Factor?
The ratio of the corresponding sides of two similar geometric figures is called the scale-factor.
Tangents to a circle from a point lying outside the circle
Two tangents can be drawn to a circle through a point outside the circle and pair of these tangents are always equal in length.