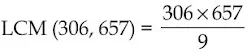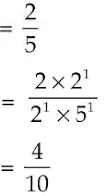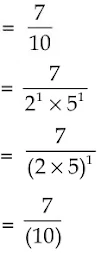NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers
Here, we have providing Class 10 Maths NCERT Solutions for Chapter 1 Real Numbers which will be beneficial for students. These solutions are updated according to 2020-21 syllabus. As NCERT Solutions are prepared by Studyrankers experts, we have taken of every steps so you can understand the concepts without any difficulty. These Real Numbers Class 10 NCERT Solutions can be really helpful in the preparation of Board exams and will provide you with in depth detail of the chapter.Page No. 7
Exercise 1.1
1. Use Euclid's division algorithm to find the HCF of:
(i) 135 and 225
(ii) 196 and 38220
(iii) 867 and 255
Answer
(i) 225 > 135 we always divide greater number with smaller one.
Divide 225 by 135 we get 1 quotient and 90 as remainder so that,
225= 135 × 1 + 90
Divide 135 by 90 we get 1 quotient and 45 as remainder so that,
135= 90 × 1 + 45
Divide 90 by 45 we get 2 quotient and no remainder so we can write it as
90 = 2 × 45+ 0
As there are no remainder so divisor 45 is our HCF.
(ii) 38220 > 196 we always divide greater number with smaller one.
Divide 38220 by 196 then we get quotient 195 and no remainder so we can write it as
38220 = 196 × 195 + 0
As there is no remainder so divisor 196 is our HCF.
(iii) 867 > 255 we always divide greater number with smaller one.
Divide 867 by 255 then we get quotient 3 and remainder is 102 so we can write it as
867 = 255 × 3 + 102
Divide 255 by 102 then we get quotient 2 and remainder is 51 so we can write it as
255 = 102 × 2 + 51
Divide 102 by 51 we get quotient 2 and no remainder so we can write it as
102 = 51 × 2 + 0
As there is no remainder so divisor 51 is our HCF.
2. Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is some integer.
Answer
Let take a as any positive integer and b = 6.
Then using Euclid’s algorithm we get a = 6q + r here r is remainder and value of q is more than or equal to 0 and r = 0, 1, 2, 3, 4, 5 because 0 ≤ r < b and the value of b is 6
So, total possible forms will 6q + 0 , 6q + 1 , 6q + 2,6q + 3, 6q + 4, 6q + 5
6q + 0
6 is divisible by 2 so it is a even number
6q + 1
6 is divisible by 2 but 1 is not divisible by 2 so it is a odd number
6q + 2
6 is divisible by 2 and 2 is also divisible by 2 so it is a even number
6q + 3
6 is divisible by 2 but 3 is not divisible by 2 so it is a odd number
6q + 4
6 is divisible by 2 and 4 is also divisible by 2 it is a even number
6q + 5
6 is divisible by 2 but 5 is not divisible by 2 so it is a odd number
So, odd numbers will in form of 6q + 1, or 6q + 3, or 6q + 5.
3. An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Answer
HCF (616, 32) will give the maximum number of columns in which they can march.
We can use Euclid's algorithm to find the HCF.
616 = 32 × 19 + 8
32 = 8 × 4 + 0
The HCF (616, 32) is 8.
Therefore, they can march in 8 columns each.
4. Use Euclid's division lemma to show that the square of any positive integer is either of form 3m or 3m + 1 for some integer m.
[Hint: Let x be any positive integer then it is of the form 3q, 3q + 1 or 3q + 2. Now square each of these and show that they can be rewritten in the form 3m or 3m + 1.]
Answer
Let a be any positive integer and b = 3.
Then a = 3q + r for some integer q ≥ 0
And r = 0, 1, 2 because 0 ≤ r < 3
Therefore, a = 3q or 3q + 1 or 3q + 2
Or,
a2 = (3q)2 or (3q + 1)2 or (3q + 2)2
a2 = (9q)2 or 9q2 + 6q + 1 or 9q2 + 12q + 4
= 3 × (3q2) or 3(3q2 + 2q) + 1 or 3(3q2 + 4q + 1) + 1
= 3k1 or 3k2 + 1 or 3k3 + 1
Where k1, k2, and k3 are some positive integers
Hence, it can be said that the square of any positive integer is either of the form 3m or 3m + 1.
5. Use Euclid's division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.
Answer
Let a be any positive integer and b = 3
a = 3q + r, where q ≥ 0 and 0 ≤ r < 3
∴ a = 3q or 3q + 1 or 3q + 2
Therefore, every number can be represented as these three forms. There are three cases.
Case 1: When a = 3q,
a3 = (3q)3 = 27q3 = 9(3q)3 = 9m,
where, m is an integer such that m = 3q3
Case 2: When a = 3q + 1,
a3 = (3q +1)3
a3= 27q3 + 27q2 + 9q + 1
a3 = 9(3q3 + 3q2 + q) + 1
a3 = 9m + 1
where, m is an integer such that m = (3q3 + 3q2 + q)
Case 3: When a = 3q + 2,
a3 = (3q +2)3
a3= 27q3 + 54q2 + 36q + 8
a3 = 9(3q3 + 6q2 + 4q) + 8
a3 = 9m + 8
where m is an integer such that m = (3q3 + 6q2 + 4q)
Therefore, the cube of any positive integer is of the form 9m, 9m + 1, or 9m + 8.
Page No: 11
Exercise 1.2
1. Express each number as product of its prime factors:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
Answer
(i) 140 = 2 × 2 × 5 × 7 = 22 × 5 × 7
(ii) 156 = 2 × 2 × 3 × 13 = 22 × 3 × 13
(iii) 3825 = 3 × 3 × 5 × 5 × 17 = 32 × 52 × 17
(iv) 5005 = 5 × 7 × 11 × 13
(v) 7429 = 17 × 19 × 23
2. Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers.
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54
Answer
(i) 26 = 2 × 13
91 =7 × 13
HCF = 13
LCM =2 × 7 × 13 =182
Product of two numbers 26 × 91 = 2366
Product of HCF and LCM 13 × 182 = 2366
Hence, product of two numbers = product of HCF × LCM
(ii) 510 = 2 × 3 × 5 × 17
92 = 2 × 2 × 23
HCF = 2
LCM =2 × 2 × 3 × 5 × 17 × 23 = 23460
Product of two numbers 510 × 92 = 46920
Product of HCF and LCM 2 × 23460 = 46920
Hence, product of two numbers = product of HCF × LCM
(iii) 336 = 2 × 2 × 2 × 2 × 3 × 7
54 = 2 × 3 × 3 × 3
HCF = 2 × 3 = 6
LCM = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 7 =3024
Product of two numbers 336 × 54 =18144
Product of HCF and LCM 6 × 3024 = 18144
Hence, product of two numbers = product of HCF × LCM.
3. Find the LCM and HCF of the following integers by applying the prime factorization method.
(i) 12, 15 and 21
(ii) 17, 23 and 29
(iii) 8, 9 and 25
Answer
(i) 12 = 2 × 2 × 3
15 = 3 × 5
21 =3 × 7
HCF = 3
LCM = 2 × 2 × 3 × 5 × 7 = 420
(ii) 17 = 1 × 17
23 = 1 × 23
29 = 1 × 29
HCF = 1
LCM = 1 × 17 × 19 × 23 = 11339
(iii) 8 =1 × 2 × 2 × 2
9 =1 × 3 × 3
25 =1 × 5 × 5
HCF =1
LCM = 1 × 2 × 2 × 2 × 3 × 3 × 5 × 5 = 1800
4. Given that HCF (306, 657) = 9, find LCM (306, 657).
Answer
We have the formula that,
Product of LCM and HCF = product of number
LCM × 9 = 306 × 657
Divide both side by 9 we get,
⇒ LCM = 34 × 657 = 22338
5. Check whether 6n can end with the digit 0 for any natural number n.
Answer
If any digit has last digit 10 that means it is divisible by 10 and the factors of 10 = 2 × 5.
So, value 6n should be divisible by 2 and 5 both.
6n is divisible by 2 but not divisible by 5 as the prime factors of 6 are 2 and 3.
So, it can not end with 0.
6. Explain why 7×11×13 + 13 and 7×6×5×4×3×2×1 + 5 are composite numbers.
Answer
7 × 11 × 13 + 13
Taking 13 common, we get
13 (7×11 +1 )
⇒ 13(77 + 1 )
⇒ 13 (78)
It is product of two numbers and both numbers are more than 1 so it is a composite number.
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
Taking 5 common, we get
5(7 × 6 × 4 × 3 × 2 × 1 +1)
⇒ 5(1008 + 1)
⇒ 5(1009)
It is product of two numbers and both numbers are more than 1 so it is a composite number.
7. There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point.
Answer
They will be meet again after LCM of both values at the starting point.
18 = 2 × 3 × 3
12 = 2 × 2 × 3
LCM = 2 × 2 × 3 × 3 = 36
Therefore, they will meet together at the starting point after 36 minutes.
Page No: 14
Exercise 1.3
1. Prove that √5 is irrational.
Answer
Let us take √5 as rational number
If a and b are two co prime number and b is not equal to 0.
We can write √5 = a/b
Multiply by b both side we get,
b√5 = a
To remove root, Squaring on both sides, we get
5b2 = a2 …(i)
Therefore, 5 divides a2 and according to theorem of rational number, for any prime number p which is divides a2 then it will divide a also.
That means 5 will divide a. So we can write,
a = 5c
Putting value of a in equation (i) we get
5b2 = (5c)2
⇒ 5b2 = 25c2
Divide by 25 we get,
b2/5 = c2
Similarly, we get that b will divide by 5 and we have already get that a is divide by 5 but a and b are co prime number. So it contradicts.
Hence, √5 is not a rational number, it is irrational.
2. Prove that 3 + 2√5 is irrational.
Answer
Let take that 3 + 2√5 is a rational number.
So we can write this number as,
3 + 2√5 = a/b
Here, a and b are two co prime number and b is not equal to 0
Subtract 3 both sides we get
2√5 = a/b – 3
⇒ 2√5 = (a-3b)/b
Now, divide by 2, we get
√5 = (a-3b)/2b
Here, a and b are integer so (a-3b)/2b is a rational number so √5 should be a rational number. But √5 is a irrational number, so it contradicts.
Hence, 3 + 2√5 is a irrational number.
3. Prove that the following are irrationals:
(i) 1/√2
(ii) 7√5
(iii) 6 + √2
Answer
(i) Let take that 1/√2 is a rational number.
So, we can write this number as
1/√2 = a/bHere, a and b are two co prime number and b is not equal to 0
Multiply by √2 both sides we get,
1 = (a√2)/b
Now, multiply by b
b = a√2
Divide by a we get
b/a = √2Here, a and b are integer, so b/a is a rational number. So, √2 should be a rational number
But √2 is a irrational number so it contradicts.
Hence, 1/√2 is a irrational number
So we can write this number as
7√5 = a/b
Here, a and b are two co prime number and b is not equal to 0
Divide by 7 we get
√5 = a/(7b)
Here, a and b are integer so a/7b is a rational number so √5 should be a rational number but √5 is a irrational number so it contradicts.
Hence, 7√5 is a irrational number.
(iii) Let take that 6 + √2 is a rational number.
So we can write this number as
6 + √2 = a/b
Here, a and b are two co prime number and b is not equal to 0
Subtract 6 both side we get
√2 = a/b – 6
⇒ √2 = (a - 6b)/b
Here, a and b are integer so (a-6b)/b is a rational number, So, √2 should be a rational number.
But √2 is a irrational number so it contradicts.
Hence, 6 + √2 is a irrational number.
Page No: 17
Exercise 1.4
1. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
(i) 13/3125
(ii) 17/8
(iii) 64/455
(iv) 15/1600
(v) 29/343
(vi) 23/23 × 52
(vii) 129/22 × 57 × 75
(viii) 6/15
(ix) 35/50
(x) 77/210
Answer
(i) 13/3125
Factorize the denominator we get
3125 =5 × 5 × 5 × 5 × 5 = 55
So, denominator is in form of 5m so it is terminating.
(ii) 17/8
Factorize the denominator we get,
8 =2 × 2 × 2 = 23
So, denominator is in form of 2m so it is terminating.
(iii) 64/455
Factorize the denominator we get,
455 = 5 × 7 × 13
There are 7 and 13 also in denominator so denominator is not in form of 2m × 5n. So, it is not terminating.
(iv) 15/1600
Factorize the denominator we get,
1600 = 2 × 2 × 2 ×2 × 2 × 2 × 5 × 5 = 26 × 52
So, denominator is in form of 2m × 5n
Hence, it is terminating.
(v) 29/343
Factorize the denominator we get,
343 = 7 × 7 × 7 = 73
There are 7 also in denominator so denominator is not in form of 2m × 5n
Hence, it is non-terminating.
(vi) 23/(23 × 52)
Denominator is in form of 2m × 5n
Hence, it is terminating.
(vii) 129/(22 × 57 × 75 )
Denominator has 7 in denominator so denominator is not in form of 2m × 5n
Hence, it is none terminating.
(viii) 6/15
Divide nominator and denominator both by 3 we get 2/5
Denominator is in form of 5m so it is terminating.
(ix) 35/50 divide denominator and nominator both by 5 we get 7/10
Factorize the denominator we get,
10 = 2 × 5
So, denominator is in form of 2m × 5n so it is terminating.
(x) 77/210
Simplify it by dividing nominator and denominator both by 7 we get, 11/30
Factorize the denominator we get,
30 = 2 × 3 × 5
Denominator has 3 also in denominator so denominator is not in form of 2m × 5n
Hence, it is none terminating.
Page No: 18
2. Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.
Answer
(i) 13/3125
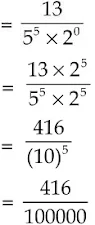
= 0.00416
(ii) 17/8
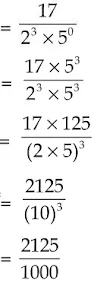
= 2.125
(iv) 15/1600

= 0.009375
(vi) 23/2352
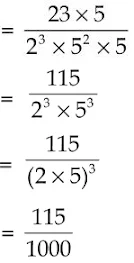
= 0.115
(viii) 6/15
Dividing numerator and denominator by 3.
= 0.4
(ix) 35/50
Dividing numerator and denominator by 5.
= 0.7.
3. The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form p , q you say about the prime factors of q?
(i) 43.123456789
(ii) 0.120120012000120000...
(iii) 43.123456789
Answer
(i) Since this number has a terminating decimal expansion, it is a rational number of the form p/q, and q is of the form 2m × 5n.
(ii) The decimal expansion is neither terminating nor recurring. Therefore, the given number is an irrational number.
(iii) Since the decimal expansion is non-terminating recurring, the given number is a rational number of the form p/q, and q is not of the form 2m × 5n.

Chapterwise NCERT Solutions for Class 10 Maths
NCERT Solutions for Class 10 Maths Chapter 1 - Real Numbers
In chapter 1 Real Numbers, we will restart our exploration of the world of real numbers. We will study Euclid’s division algorithm and the Fundamental Theorem of Arithmetic. Also, we will see decimal representation of real numbers.
Euclid's Division Algorithm is a technique to compute HCF or GCD (greatest common divisor) of two given positive integers saya and b (a > b) by successive use of Euclid's division lemma.
The Fundamental Theorem of Arithmetic, on the other hand, has to do something with multiplication of positive integers. It says very composite number can be factorised as a product of primes, and this factorisation is unique, apart from the order in which prime factors occur.
We have also provided Notes of Chapter 1 Real Numbers Class 10 Maths, MCQ Questions of Chapter 1 Real Numbers which will supplement your preparation in a better way.