Extra Questions Answers for Class 6 Maths Chapter 6 Perimeter and Area - Ganita Prakash
Chapter 6 Perimeter and Area Extra Questions Answers for Class 6 Maths is provided here by studyrankers. All the questions are crafted by our experts by keeping in mind that all the important points must be covered. You can also Download PDF of Class 6 Maths Chapter 6 Perimeter and Area Extra Questions which will boost the student confidence and help in solving the exercises and questions from the chapter. The chapter is taken from the new NCERT Mathematics textbook, Ganita Prakash.
These Revision Notes for Class 6 Maths will develop you understanding of the chapter and help in gaining good marks in the examinations. We have also provided Chapter 6 Perimeter and Area NCERT Solutions which will help you in completing your homework on time. These NCERT Solutions will help an individual to increase concentration and you can solve questions of supplementary books easily. Students can also check Revision Notes for Perimeter and Area Class 6 Maths to prepare for their examination completely.
Important Questions for Chapter 6 Perimeter and Area Class 6 Maths
Multiple Choice Questions
Question 1. What is the perimeter of a square with a side length of 5 cm?
(a) 5 cm
(b) 10 cm
(c) 15 cm
(d) 20 cm
Answer
(d) 20 cm
Perimeter of a square = 4 × side length
= 4 × 5
= 20 cm.
Question 2. The area of a rectangle is 24 cm², and its length is 8 cm. What is the width of the rectangle?
(a) 2 cm
(b) 3 cm
(c) 4 cm
(d) 5 cm
Answer
(c) 4 cm
Area of a rectangle = length × width
24 = 8 × width
⇒ Width = 24 ÷ 8 = 3 cm.
Question 3. A triangle has a base of 10 cm and a height of 6 cm. What is its area?
(a) 30 cm2
(b) 60 cm2
(c) 50 cm2
(d) 15 cm2
Answer
(a) 30 cm2
Area of a triangle = (1/2) × base × height
= (1/2) × 10 × 6
= 30 cm2.
Question 4. What is the perimeter of a rectangle with a length of 15 cm and a width of 10 cm?
(a) 25 cm
(b) 30 cm
(c) 40 cm
(d) 50 cm
Answer
(d) 50 cm
The perimeter is 2 × (length + width)
= 2 × (15 cm + 10 cm)
= 50 cm.
Question 5. A square has a perimeter of 24 cm. What is the length of one side?
(a) 4 cm
(b) 6 cm
(c) 8 cm
(d) 12 cm
Answer
(b) 6 cm
The side length of square = perimeter/4,
So, 24 cm/4 = 6 cm.
Question 6. The area of a rectangle is 54 square units. If its length is 9 units, what is its width?
(a) 5 units
(b) 6 units
(c) 7 units
(d) 8 units
Answer
(b) 6 units
The width is area ÷ length, so 54 square units ÷ 9 units = 6 units.
Question 7. A triangle has a perimeter of 20 cm. If two of its sides are 8 cm and 6 cm, what is the length of the third side?
(a) 4 cm
(b) 6 cm
(c) 8 cm
(d) 10 cm
Answer
(a) 6 cm
The third side is calculated by subtracting the sum of the other two sides from the perimeter: 20 cm - (8 cm + 6 cm) = 6 cm.
Question 8. A rectangular park is 30 meters long and 20 meters wide. What is the area of the park?
(a) 50 square meters
(b) 100 square meters
(c) 400 square meters
(d) 600 square meters
Answer
(d) 600 square meters
The area is length × width, so 30 meters × 20 meters = 600 square meters.
Fill in the Blanks
Question 1. The perimeter of a square with a side length of 5 cm is ______.
Answer
20 cm
The perimeter of a square is calculated as 4 × side length, so 4 × 5 cm = 20 cm.
Question 2. A rectangular field has a length of 10 m and a width of 5 m. The perimeter of the field is ______.
Answer
30 m
The perimeter of a rectangle is 2 × (length + width), so 2 × (10 m + 5 m) = 30 m.
Question 3. If the area of a square is 64 square units, the length of one side is _____ units.
Answer
8 units
The area of a square is side length × side length, so the side length is √64 = 8 units.
Question 4. The perimeter of a triangle with sides of 7 cm, 8 cm, and 9 cm is _______.
Answer
24 cm
The perimeter of a triangle is the sum of the lengths of its sides. So, 7 cm + 8 cm + 9 cm = 24 cm.
Question 5. A rectangular garden has an area of 48 square meters and a width of 6 meters. The length of the garden is ______ meters.
Answer
8 meters
The area of a rectangle is length × width, so 48 square meters ÷ 6 meters = 8 meters.
Question 6. The length of boundary of a plane figure is called_____
Answer
Perimeter
Question 7. Perimeter of rectangle = ____?
Answer
2(l+b)
We know that the Perimeter of the rectangle = 2(l+b),
Here, l = length, b = breadth
Question 8. Perimeter of square = ___?
Answer
4×side
We know that the perimeter is the length of the boundaries of a figure.
Square has four sides.
Therefore, Perimeter of square = 4×side
Question 9. Area of rectangle = (a)____× (b)_____square units.
Answer
(a) Length
(b) Breadth
We know that area of rectangle = length×breadth
Question 10. Area of square = (a)____× (b)_____ square units.
Answer
(a) Side
(b) Side
We know that area of a square is side×side
True/False
Question 1. The area of a triangle can be found using the formula Area
Answer
True
Question 2. In an equilateral triangle, the perimeter is calculated by multiplying the side length by 4.
Answer
False
The perimeter of an equilateral triangle is calculated by multiplying the side length by 3.
Question 3. To determine the amount of material needed to cover a square-shaped frame, Rohan needs to calculate the area of the frame.
Answer
False
To cover the border of a square-shaped frame, Rohan needs to calculate the perimeter, not the area. The perimeter will give the total length of the border material needed. The area of the frame would give the total space covered by the frame, not the length of the border material.
Question 4. The area of a rectangle is always greater than its perimeter.
Answer
False
The area of a rectangle depends on its length and width, and can be less than, equal to, or greater than the perimeter depending on the dimensions.
Question 5. The perimeter of a square is four times the length of one side.
Answer
True
The formula for the perimeter of a square is 4 × side length.
Question 6. A triangle with all sides equal has a perimeter that is three times the length of one side.
Answer
True
The perimeter of an equilateral triangle is 3 × side length.
Question 7. If a rectangle has an area of 36 square units and a width of 4 units, its length must be 9 units.
Answer
False
The length is calculated as area ÷ width, so it should be 36 ÷ 4 = 9 units.
Question 8. A square and a rectangle with the same perimeter have the same area.
Answer
False
The area of the shapes depends on the side lengths, so they can have different areas even if the perimeter is the same.
Solve this
Question 1. Draw a square with a side length of 5 units. Calculate its perimeter and area.
Answer

Perimeter = 20 units, Area = 25 square units
The perimeter is 4 × side length = 4 × 5 units = 20 units.
The area is side length × side length = 5 units × 5 units = 25 square units.
Question 2. A square-shaped playground has a side length of 150 m. The cost of fencing the playground is ₹12 per meter. What will be the total cost of fencing?
Answer
Perimeter of a square = 4 × side
= 4 × 150
= 600 m
Cost per meter = ₹12
Total cost = 600 × 12
= ₹7,200
Question 3. A farmer wants to plant a rectangular field with a length of 100 meters and a width of 40 meters. What is the area of the field?
Answer
4000 square meters
The area is length × width = 100 meters × 40 meters = 4000 square meters.
Question 4. A rectangular parking area is 120 m long and 60 m wide. If each car requires 20 sq. m of space, what is the maximum number of cars that can be parked in the area?
Answer
Area of the parking lot = 120 × 60 = 7,200 sq. m
Each car requires 20 sq. m
Maximum number of cars = 7200 ÷ 20
= 360 cars
Question 5. Draw a rectangle with a length of 8 units and a width of 4 units. Calculate the perimeter and area.
Answer
The perimeter is 2 × (length + width)
= 2 × (8 units + 4 units)
= 24 units.
The area is length × width = 8 units × 4 units
= 32 square units.
Crossword
Question 6. Complete the crossword:
Across →
(1) Perimeter (in cm) of an equilateral triangle of side 220 cm.
(3) Perimeter (in cm) of a regular hexagon of side 84 cm.
(5) 4 m 25 cm = ____ cm.
Down ↓
(2) Perimeter (in cm) of a regular pentagon of side 120 cm.
(4) Number of unit squares (sq. cm.) enclosed in a square of side 22 cm.
(6) Distance covered along a triangular park (in 1 round) measuring 12 m, 20 m and 23 m. (distance in m)
Answer
(1) 660
(2) 600
(3) 504
(4) 484
(5) 425
(6) 55
Question 7. Which of the following figure has a greater perimeter?
Answer
(i) Perimeter of the square = 4×side
= 4×4 cm = 16 cm
(ii) Perimeter of the rectangle
= 2 [length + breadth]
= 2[8 cm + 3 cm]
= 2×11 cm = 22 cm
Since 22 cm > 16 cm
∴ Rectangle has greater perimeter than the square.
Question 8. Find the total distance covered by an athlete in taking 2 rounds of a rectangular park of length 150 m and breadth 80 m.
Answer
Given the breadth of the rectangular park b= 80m and Length l= 150 m
The perimeter of the park =2 (b+l) =2×( 80 +150) = 2× 230 = 460m
Given: The athlete takes 2 rounds around the rectangular park
So, the total distance covered by the athlete = 2× 460 m = 920 m
Question 9. A tailor wants to put lace around a square tablecloth of side 20 cm. He bought 1 m lace from the market. Find the length of lace left with him after completing the task.
Answer
Side = 20cm
Perimeter of Square: S×4 = 20×4 = 80 cm
Length of cloth = 1m = 100 cm
Cloth left: 100 - 80 = 20cm
Question 10. The length of a rectangular park is 50 m and its area is 650 m2. Find its breadth.
Answer
Length = 50m
Area = 650 m
So, According to the question:
Area of rectangle= Length×Breadth
⇒ 650 = 50×Breadth
⇒ 50×Breadth = 650
⇒ Breadth = 650/50
⇒ Breadth = 13m
Question 11. Find the number of square tiles required to cover the floor of a room whose length is 4 m and width 3 m, if each square tile is of side 0.2 m.
Answer
To find the number of square tiles required to cover the floor of a room, we need to first determine the area of the room in square meters. The area of a rectangle is given by the formula:
Area = Length × Width
In this case, the length of the room is 4 m and the width is 3 m, so the area of the room is 4×3 = 12 sq m.
Next, we need to determine the area of a single square tile. The area of a square is given by the formula:
Area = Side2
In this case, the side of the square tile is 0.2 m, so the area of a single tile is 0.22 = 0.04 sq m.
To find the number of tiles required to cover the floor of the room, we can divide the area of the room by the area of a single tile:
12 sq m / 0.04 sq m = 300 tiles
Therefore, the number of square tiles required to cover the floor of the room is 300 tiles.
Question 12. Two equal sides of an isosceles triangle measure 10 cm each. Find the length of its third side if its perimeter is 32 cm.
Answer
Perimeter of the triangle = sum of all the sides of it
32 = 10 + 10 + x
(let the third side be x)
⇒ 32 = 20 + x
⇒ x = 32 - 20
⇒ x = 12cm
Question 13. A piece of string is 60 cm long. What will be the length of each side if the string is used to form:
(a) a square
(b) an equilateral triangle
(c) a regular pentagon
Answer
(a) Length of wire = 60cm
Since, the wire is used to form a square, the length of wire becomes perimeter of the square.
Perimeter = 60 cm
4 × side = 60 cm
⇒ 60/4 = 15
Side =15 cm
(b) Given
length of string=60cm
If the string is used to form an equilateral triangle then the perimeter of the triangle = length of the string
Let the side of the triangle be a
a + a + a = 60
⇒ 3a =60
⇒ 3a = 60
⇒ a = 20cm
(c) Given, regular pentagon (all sides equal)
Perimeter = 5 × side = 60 cm
Side = 12 cm
Question 14. A farmer's rectangular garden is adjacent to his house, (as shown in the figure).
The rectangular garden is 200 m long and 150 m wide. Find the cost of fencing three sides of this garden at the rate of 12 per meter.
Answer
Length of garden = 200m
Breadth of garden = 150m
Cost of fencing = 12 per meter
We have to fence only 3 sides = L+L+B
200+200+150 = 550m
Cost of Fencing = 550m = 550×12 = ₹6600
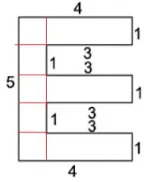
Question 15. Find the perimeter of each of the following figures: (The measures are given in cm)

Answer
(a) Perimeter = sum of all sides
5+ 1+ 2+ 2+ 2+1+5+1+2+2+2+1 = 26 cm
(b) Perimeter = sum of all sides
1+1+1+1+1+ 2+1+1+1+1+1+6 = 18 cm
(c) Perimeter = sum of all sides
13+5+12 = 30 cm
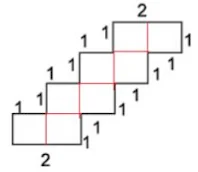
Question 16. Find the area of each of the following figures: (The measures are given in cm)
Answer
(a)
There are 3 rectangles in the picture and 5 squares
Area of one rectangle= l×b = 4X
Side of square = 1
Sides of rectangle = length = 1 and Breadth = 3
3×1= 3
No of the rectangles are 3
3x area of one rectangle = 3×3= 9
Area of square = Side2 = 1×1 = 1
No of squares 5 = 5×1= 5
Total Area = 9+5 = 14 sq.cm
(b)
No of squares = 8
Area of one square = 1×1= 1
Area of all squares = 8×1 = 8 sq.cm
(c)
Area rectangle 1 = l×b = 3×1= 3
Area of Rectangle = l×b = 4×1 = 4
Total area = 3+4 = 7 sq. cm
Question 17. Fencing the compound of a house costs ₹5452. If the rate is ₹94 per metre, find the perimeter of the compound. If the breadth is 10 m, find its length.
Answer
Cost of fencing the compound = ₹5452
and the rate of fencing = ₹94 per metre
∴ Perimeter of the compound = 5452 ÷ 94 = 58 metres
Now breadth of the compound = 10 m.
2 [length + breadth] = 58 m
∴ length + breadth = 58 + 2 m = 29 m
∴ Length of the compound = 29 m – 10 m = 19 m.
Question 18. Find the missing terms:
(a) Perimeter of a rectangle = 20 cm; breadth = 4 cm; length = ?
Answer
We know that the perimeter of a rectangle = 2(l + b)
Here, the perimeter of the rectangle = 20 cm and breadth b = 4 cm, l =?
Thus,
20 = 2(l + 4)
⇒ 20 = 2l + 8
⇒ 2l = 20 – 8 = 12
⇒ l = 12 ÷ 2 = 6 cm
Question 19. The area of a rectangular garden that is 60 m long is 1200 sq m. Find the width of the garden.
Answer
Width of the rectangular garden = area/length of the garden
= 1200/60
= 20 m
Question 20. What is the cost of tiling a rectangular plot of land 600 m long and 400 m wide at the rate of ₹10 per hundred sq m?
Answer
Here, length = 600 m and breadth = 400 m.
Hence, the area of the rectangular plot = length × breadth
= 600 × 400
= 240,000 m2
Now, cost of tiling a rectangular plot = ₹10 per 100 sq m.
Hence, the cost of tiling 240,000 sq m of rectangular plot = ₹10 × 240000 ÷ 100 = ₹24,000.
Question 21. Find the length of the third side of a triangle having a perimeter of 60 cm and having two sides of length 22 cm and 18 cm, respectively.
Answer
Let the length of the third side of the triangle be x cm. Then,
Perimeter of triangle = AB + BC + CA
⇒ 60 = 22 + 18 + x
⇒ 60 = 40 + x
⇒ x = 60 – 40
⇒ x = 20 cm
Question 22. What would be the cost of fencing a rectangular park whose length is 180 m and breadth is 130 m if the fence costs ₹50 per meter?
Answer
The length of the fence is the perimeter of the rectangular park.
Given that the length of the rectangular park = 180 m and breadth = 130 m.
Thus,
Perimeter = 2(l + b)
= 2(180 + 130)
= 2(310)
= 620 m
Now, the cost of fencing per meter = ₹50
Cost of fencing the rectangular park = ₹50 × 620 = ₹31,000
Question 23. A farmer has a rectangular field as given. He wants to fence it with 4 rounds of rope. What is the total length of rope needed?

Answer
Perimeter of the rectangular field = 2(l + b)
Here, l = 250 m, b = 180 m
Thus, P = 2(250 + 180)
= 2(430)
= 860 m
Distance covered by a farmer in one round = 860 m
Thus, total length of rope needed = 4 × 860 = 3440 m
Question 24. A rectangle with side lengths 6 cm and 4 cm is made using a wire. If the wire is straightened and then bent to form a square, what will be the length of the side of the square?
Answer
Here, the perimeter of the rectangle = 2(6 + 4)
= 2 × 10
= 20 cm
Now the wire is straightened and then bent to form a square.
Thus, perimeter of the square = 20 cm
⇒ 4a = 20 cm
⇒ a = 20 ÷ 4 = 5 cm, the required length of the side of the square.
Question 25. The floor of a room is 6 m long and 5 m wide. A square carpet whose sides are 4 m in length is laid on the floor. Find the area that is not carpeted.

Answer
We have a floor with dimensions 6 m in length and 5 m in width.
A square carpet of side 4 m.
Area of the floor = length × breadth
= 6 × 5
= 30 m2
Area of the square carpet = 4 × 4
= 16 m2
Now, we will subtract the square carpet area from the floor’s area to get the area of the floor that is not carpeted.
Hence, the area of the floor that is not carpeted = 30 – 16 = 14 m2
Thus, the area of the floor that is not carpeted is 14 m2.