Extra Question Answer for Ch 7 Fractions Class 6 Maths Ganita Prakash

Extra Questions Answers for Class 6 Maths Chapter 7 Fractions - Ganita Prakash

Chapter 7 Fractions Extra Questions Answers for Class 6 Maths is provided here by studyrankers. All the questions are crafted by our experts by keeping in mind that all the important points must be covered. You can also Download PDF of Class 6 Maths Chapter 7 Fractions Extra Questions which will boost the student confidence and help in solving the exercises and questions from the chapter. The chapter is taken from the new NCERT Mathematics textbook, Ganita Prakash.

These Revision Notes for Class 6 Maths will develop you understanding of the chapter and help in gaining good marks in the examinations. We have also provided Chapter 7 Fractions NCERT Solutions which will help you in completing your homework on time. These NCERT Solutions will help an individual to increase concentration and you can solve questions of supplementary books easily. Students can also check Revision Notes for Fractions Class 6 Maths to prepare for their examination completely.

Important Questions for Chapter 7 Fractions Class 6 Maths

Multiple Choice Questions

Question 1. What is the difference between the following fractions?

7/9 - 4/9

(a) 3/9
(b) 5/9
(c) 1/9
(d) 7/18

Answer

(b) 5/9

Since the denominators are the same (9), subtract the numerators:
7/9 - 4/9 = (7 - 4)/9 = 3/9.
Simplify the fraction:
3/9 = 1/3. Thus, the correct answer is 5/9.

Question 2. What is the sum of the following fractions?

3/4 + 5/8

(a) 5/8
(b) 7/8
(c) 3/2
(d) 1

Answer

(b) 7/8

To add fractions, first find a common denominator.
The least common denominator of 4 and 8 is 8.
Convert 3/4 to an equivalent fraction with a denominator of 8:
3/4 = 6/8.
Now add the fractions:
6/8 + 5/8 = (6 + 5)/8 = 11/8.
So, the correct sum is 7/8, as the fraction simplifies to 7/8.

Question 3. Which of the following represents 12 ?

(i) Only figure (a)
(ii) Only figure (b)
(iii) Both figures (a) and (b)
(iv) Neither figure (a) nor figure (b)

Answer

(i) Only figure (a)
As other figure doesn't divide the triangle equally.

Question 4. Which of the following pairs of fractions are equivalent?

(a) 3/5 and 6/10
(b) 4/7 and 8/12
(c) 5/8 and 10/16
(d) 2/9 and 4/8

Answer

(c) 5/8 and 10/16

To check if fractions are equivalent, cross-multiply and see if the products are equal:
For 5/8 and 10/16,
5 × 16 = 80, and 8 × 10 = 80, so the fractions are equivalent.

Fill in the Blanks

Question 1. When 4 children share 1 roti equally, each child gets _____ roti. 

Answer

1/4
When a whole item (roti) is divided into 4 equal parts, each part is 1/4 of the whole.

Question 2. A whole roti is divided into 3 equal pieces. Each piece is _____ of the roti. 

Answer

1/3
When something is divided into 3 equal parts, each part is represented as 1/3.

Question 3. If 2 chikkis are divided equally among 6 children, each child gets _____ chikki

Answer

1/3
Two rotis divided among 6 children means each child gets a fraction of 2/6 which simplifies to 1/3.

Question 4. If 1 glass of juice is equally shared between 3 children, each child gets _____ glass of juice. 

Answer

1/3
Sharing 1 glass equally among 3 children results in each child receiving 1/3 of the glass.

Question 5. To compare fractions with different denominators, we convert them to have the same ______. 

Answer

denominator
Fractions need to be converted to have the same denominator for easy comparison.

True or False

Question 1. The fraction 1/2 is smaller than 1/4. 

Answer

False
1/2 represents a larger portion than 1/4 when comparing fractions of the same whole.

Question 2. When 5 children share 2 cakes equally, each child's share is 2/5 of a cake. 

Answer

True
Dividing 2 cakes among 5 children gives each child 2/5 of a cake.

Question 3. The fraction 3/6 is equivalent to 1/2. 

Answer

True
3/6 simplifies to 1/2, making them equivalent fractions.

Question 4. The number line can only represent whole numbers, not fractions. 

Answer

False
Fractions can be represented on a number line just like whole numbers.

Question 5. Adding 1/4 and 2/4 results in 3/4. 

Answer

True

When fractions have the same denominator, their numerators can be added directly.

Match the Following

Column A	Column B
1/3	A. Three-fourths
2/5	B. One-third
¾	C. Two-fifths
½	D. One-half
¼	E. One-fourth

Answer

Solve this:

Question 1. Are 6/9, 12/18, 15/25 equivalent fraction? Why?

Solution

Here, the simplest form of 6/9 is:

The simplest form of 12/18 is:

The simplest form of 15/25 is:

Hence, 6/9, 12/18, 15/25 are not equivalent fractions because their simplest forms are different.

Question 2. Add the following fractions and express the result as a mixed fraction:

7/4 + 5/6 + 8/3

Solution

Given,

Here, the LCM of 4, 6 and 3 is 12.

Now, expressing as equivalent fractions with denominator 12, we get:

Breaking into a mixed fraction:

Hence, the sum 5¼

Question 3. Subtract as indicated:

15/4 from 11/3

Solution

Given,

Here, the LCM of 3 and 4 is 12.

Fractional unit for both fractions should be 1/12.

Question 4. Compare the following fractions and justify your answers:

7/4, 5/3

Solution

Given fractions are 7/4 and 5/3.

Here, the LCM of denominators 4 and 3 is 12.

Now, multiplying and dividing 7/4 by 3 and 5/3 by 4:

Since, 21/12 > 20/12.

Word Problems 

Question 1. Aman mixes 7/9 liters of lemon juice with 5/6 liters of orange juice to make fruit punch. What is the total volume of fruit punch he has made?

Solution

Given quantity of lemon juice = 7/9 litres

Given quantity of orange juice = 5/6 litres

Total volume of fruit punch made:

Here, the LCM of 9 and 6 is 18.

Now, expressing as equivalent fractions with denominator 18, we get:

Breaking into a mixed fraction:

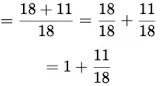
Question 2. Rina's school is 11/15 km from her home. She rides her bicycle for 2/5 km from her home daily and then walks the remaining distance to reach her school. How much distance does she walk daily?

Solution

Given distance between Rina’s school and home = 11/15 km

Distance covered by Rina on her bicycle = 2/5 km

LCM of 15 and 5 is 15.

Now, converting into equivalent fractions:

So, Rina walks 1/3 km daily to reach her school.

Question 3. Mohan takes 5/3 minutes to complete a swimming lap, while his friend Sohan takes 8/5 minutes to do the same. Who completes the lap faster and by how much?

Solution

Time taken by Mohan to complete 1 lap = 5/3 minutes

Time taken by Sohan to complete 1 lap = 8/5 minutes

To determine who is faster, we need to compare 5/3 and 8/5.

Here, the LCM of 3 and 5 is 15.

Now, expressing fractions with denominator 15, we get:

Mohan takes more time than Sohan.

Now, finding the difference:

So, Sohan takes 1/15 minutes less than Mohan.

Question 4. Write the fraction representing the shaded portion. 

(i) 

(ii) 

Solution

(i) Total number of boxes = 12 
Total number to shaded portion = 7

Therefore, fraction representing the shaded portion = 712 

(ii) Total parts = 4
Total number to shaded parts = 3

Therefore, fraction representing the shaded portion = 34

Question 5. Colour the part according to the given fraction:

(i) 

(ii) 

Solution

(i) 

(ii) 

Question 6. Write natural numbers from 1 to 15: ______

(i) What fraction of them are prime numbers?
(ii) What fraction of them are composite numbers?

Solution

The natural numbers from 1 to 15 are:1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15

(i) The prime numbers are: 2, 3, 5, 7, 11, 13.
So, there are 6 prime numbers.

= 615 = 25

(ii) The composite numbers are:4, 6, 8, 9, 10, 12, 14, 15.
So, there are 8 composite numbers.

= 815

Question 7. Identify the following fractions:

(i) 6 hours of a day.
(ii) 750 gms of a kilogram.

Solution

(i)A day has 24 hours. 
Fraction = 624 = 14

(ii) A kilogram is equal to 1000 grams.
Fraction = 7501000 = 34

Question 8. Fill the following blanks with <, > or = 

(i) 12 ____ 15

(ii) 33 ____ 36

(iii) 14 ____ 28

Solution

(i) >

12 = 0.5 and 15 = 0.2, so 0.5 > 0.2.

(ii) >

Explanation: 33 = 1 and 36 = 0.5, so 1 > 0.5.

(iii) =

Explanation: 14 = 0.25 and 28 = 0.25, so 0.25 = 0.25.

Question 9. Put the following set of fractions in descending order:

(i) 15, 35, 135, 95, 125
(ii) 37, 311, 32, 35, 310

Solution

(i) Since the denominators are the same we will compare the numerators, then the order becomes:
135 > 125 > 95 > 35 > 15

(ii) The smaller the denominator, the larger the fraction:
32 > 35 > 37 > 310 > 311

Question 10. Represent 58 and 38 on the number line.

Solution

Question 11. Rita has a pizza with 8 slices. She ate 3 pieces out of it. Sita eats ¼ of the same pizza. Who eats more and by how much?

Solution

Rita eats more pizza than Sita.
Rita eats 38 - 28 = 18 more pizza than Sita.

Question 12. Is it true or false for the following? If not then mention the correct options (<, > or =) 

(i) 14 = 1

(ii) 55 = 1

(iii) 06 < 1

(iv) 78 < 1

Solution

(i) False, <

14 means 1 divided by 4, which equals 0.25.
So, 14 ≠ 1, and this statement is false.

(ii) True
55 means 5 divided by 5, which equals 1.
So, 55 = 1, and this statement is true.

(iii) False, <
06 means 0 divided by 6, which equals 0.
Since 0 is less than 1, the statement is true.

(iv) True
78 is 0.875, which is less than 1.
So, 78 < 1, and the statement is true.

Question 13. Find the equivalent fraction of 35, with

(i) Numerator 27
(ii) Denominator 25

Solution

(i) We need to find a number to multiply 3 by to get 27.
So, 3×9=27

Now, we multiply the denominator by the same number, 9, to maintain the equality of the fraction:
35 × 99 = 2745

So, the equivalent fraction with numerator 27 is 2745.

(ii) We need to find a number to multiply 5 by to get 25.
So, 5×5=25

Now, we multiply the numerator by the same number, 5, to maintain the equality of the fraction:
35 × 55 = 1525

So, the equivalent fraction with denominator 25 is 1525.

Question 14. Reduce to the simplest form: 

(i) 15060

(ii) 3672

(iii) 5125

Solution

(i) The prime factorization of 150 is 2 × 3 × 5², and the prime factorization of 60 is 2² × 3 × 5.

The common factors are 2 × 3 × 5 = 30.
Now, divide both the numerator and denominator by 30:
15060 = 150 ÷ 3060 ÷ 30 = 52.
The simplest form of 15060 is 52.

(ii) The prime factorization of 36 is 2² × 3², and the prime factorization of 72 is 2³ × 3². 

The common factors are 2² × 3² = 36.
Now, divide both the numerator and denominator by 36:
3672 = 36 ÷ 3672 ÷ 36 = 12.
The simplest form of 3672 is 12.

(iii) The prime factorization of 5 is 5, and the prime factorization of 125 is 5³. 

The common factor is 5.

Now, divide both the numerator and denominator by 5:
5125 = 5 ÷ 5125 ÷ 5 = 125.

The simplest form of 5125 is 125.

Question 15. Match the following:

Solution

(i) ↔ (b)
(ii) ↔ (d)
(iii) ↔ (a)
(iv) ↔ (c)

Question 16. Complete the addition subtraction box.

Solution

Question 17. Fill in the boxes:

(i) 

(ii) 

(iii) 

Solution

(i) 2 (1/5)

(ii) 5/8

(iii) 1/6

Question 18. Four friends ordered 5 glasses of lemonade and shared it equally among themselves. Each one drank ____ glass of lemonade.

Solution

Amount of lemonade consumed by four friends = 5 glasses.
Amount of lemonade consumed by each friend = 5/4 glass.
Hence, each one drank 5/4 glass of lemonade.​​

Question 19. 8 pencils divided among 4 students is the same as pencils divided among students. So, 8/4 = _____.

Solution

The total number of pencils is 8, and there are 4 students.
To find how many pencils each student gets, divide 8 by 4.
8 ÷ 4 = 2
Hence, each student gets 2 pencils.

Question 20. Carry out the following subtractions using Brahmagupta’s method: 13/20 − 7/20.

Solution

Given 13/20 − 7/20
Fractional unit for both fractions is 1/20, then
13/20 − 7/20 
= (13 − 7)/20 
= 6/20 
= 3/10

Question 21. Add the following fractions: 5/8 + 3/4 using Brahmagupta’s method:

Solution

Here, 5/8 and 3/4
Now, LCM of 8 and 4 is 8.
Expressing as equivalent fractions with denominators 8, we get:
= 5 × 1 / 8 × 1 + 3 × 2 / 4 × 2
= 5/8 + 6/8
= 11/8
= 8/8 + 3/8

Question 22. Ravi is in a group where 3 cakes were divided equally among 6 children. Each cake gets divided into 6 parts, and Ravi gets one part from each cake.

How much cake does Ravi get in total?

Solution

Each cake is divided into 6 parts, and Ravi gets one part from each cake.
Hence, Ravi gets:
1/6 + 1/6 + 1/6 = 3/6 = 1/2

So, Ravi gets 1/2 of the total amount of cake.

Question 23. A farmer has 6 kg of rice divided equally into 4 bags. What is the amount of rice in each bag?

Solution

Here, the amount of rice per bag is:
6 kg ÷ 4 bags = 6/4 = 3/2 kg per bag
Let x be the number of bags for 15 kg of rice, where each bag contains the same amount of rice.
Then,
15 kg ÷ x bags = 3/2 kg per bag
Now, solve for x:
12 ÷ x = 3/2
⇒ 12 × 2 = 3 × x
⇒ 24 = 3x
⇒ x = 24 ÷ 3
⇒ x = 8
Hence, 8 bags are required to store 15 kg of rice when each bag contains 3/2 kg of rice.

Question 24. Find equivalent fractions for the given pairs of fractions such that the fractional units are the same.

(a) 4/3 and 5/6

(b) 7/4 and 3/8

Solution

(a) Given: the fractions are 4/3 and 5/6.

Here, the denominators are 3 and 6.
The least common multiple of 3 and 6 is 6.

Hence for both fractions, let's have the same denominator of 6.
Now for 4/3, multiply both the numerator and the denominator by 2.
4/3 = (4 × 2)/(3 × 2) = 8/6

For 5/6, the denominator is already 6, so we keep it as it is. 5/6

Hence, the equivalent fractions with the same denominator are: 8/6 and 5/6.

(b) Given: the fractions are 7/4 and 3/8.

Here, the denominators are 4 and 8.
The least common multiple of 4 and 8 is 8.

Hence for both fractions, let's have the same denominator of 8.
Now for 7/4, multiply both the numerator and the denominator by 2.

7/4 = (7×2)/(4×2) = 14/8

For 3/8, the denominator is already 8, so we keep it as it is. 3/8

Hence, the equivalent fractions with the same denominator are: 14/8 and 3/8

Question 25. Compare the following fractions and justify your answers:

(a) 12/5 and 7/3

(b) 5/6 and 8/9

Solution

(a) Given the fractions are 12/5 and 7/3.

Here, the LCM of denominators 5 and 3 is 15.
Then, multiplying and dividing 12/5 by 3 and 7/3 by 5, we get:
(12×3)/(5×3) = 36/15
(7×5)/(3×5) = 35/15
Hence,
36/15 > 35/15
Therefore,
12/5 > 7/3

(b) Given fractions are 5/6 and 8/9.

Here, the LCM of denominators 6 and 9 is 18.
Then, multiplying and dividing 5/6 by 3 and 8/9 by 2, we get:
(5×3)/(6×3) = 15/18
(8×2)/(9×2) = 16/18
Hence,
15/18 < 16/18
Therefore,
5/6 < 8/9