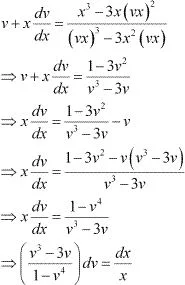Class 12 Maths NCERT Solutions for Chapter 9 Differential Equations Miscellaneous Exercise

Differential Equations Miscellaneous Exercise Solutions
1. For differential equations given below, indicate its order and degree (if defined).
(i) (d2y/dx2 ) + 5x (dy/dx)2 – 6y = log x
(ii) (dy/dx)3 + 4 (dy/dx)2 + 7y = sin x
(iii) (d4y/dx4 ) - sin (d3y/dx3 ) = 0
Solution
(i) The differential equation is given as :
The highest order derivative present in the differential equation is d2y/dx2. Thus, its order is two . The highest power raised to d2y/dx2 is one. Hence, its degree is one.
(ii) The differential equation is given as :
The highest order derivative present in the differential equation is dy/dx. Thus, its order is one. The highest power raised to dy/dx is three. Hence, its degree is three.
(iii) The differential equation is given as :
(d4y/dx4) - sin(d3y/dx3) = 0
The highest order derivative present in the differential equation is d4y/dx4. Thus, its order is four.
However, the given differential equation is not a polynomial equation. Hence, its degree is not defined.
2. For given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
(i) y = aex + be-x + x2 : x (d2y/dx2) + 2(dy/dx) - xy + x2 - 2 = 0
(ii) y = ex (a cos x + b sin x) : d2 y/dx2 - 2(dy/dx) + 2y = 0
(iii) y = x sin 3x : (d2y/dx2) + 9y - 6cos 3x = 0
(iv) x2 = 2y2 log y: (x2 + y2) dy/dx - xy = 0
Solution
(i) xy = aex + be-x + x2
Differentiating both sides w.r.t. x we get
Hence, the given function is a solution of the corresponding differential equation.
(ii) y = ex (a cos x + b sin x) = aex cos x + bex sin x.
Differentiating both sides with respect to x, we get :
⇒ dy/dx = (a + b)ex cos x + (b - a)ex sin x
Again, differentiating both sides with respect to x, we get ;
Now, on substituting the values of d2y/dx2 and dy/dx in the L.H.S. of the given differential equation, we get :
= 2ex (b cos x - a sin x) - 2ex [(a + b) cos x + (b - a) sin x] + 2ex (a cos x + b sin x)
= ex [(2b - 2a - 2b + 2a) cos x] + ex [(-2a - 2b + 2a + 2b) sin x]
= 0
Hence, the given function is a solution of the corresponding differential equation.
(iii) y = x sin3x
Differentiating both sides with respect to x, we get :
Substituting the value of d2 y/dx2 in the L.H.S. of the given differential equation, we get :
d2y/dx2 + 9y - 6 cos 3x
= (6.cos 3x - 9x sin 3x) + 9x sin 3x - 6 cos 3x
= 0
Hence, the given function is a solution of the corresponding differential equation.
(iv) x2 = 2y2 log y
Differentiating both sides with respect to x, we get :
Substituting the value of dy/dx in the L.H.S. of the given differential equation, we get :
= xy - xy
= 0
Hence, the given function is a solution of the corresponding differential equation.
3. Form the differential equation representing the family of curves given by (x – a)2 + 2y2 = a2, where a is an arbitrary constant.
Solution
(x - a)2 + 2y2 = a2
⇒ x2 + a2 - 2ax + 2y2 = a2
⇒ 2y2 = 2ax - x2 ...(1)
Differentiating with respect to x, we get :
From equation (1), we get :
2ax = 2y2 + x2
On substituting this value in equation (2), we get :
Hence, the differential equation of the family of curves is given as dy/dx = (2y2 - x2)/4xy.
4. Form the differential equation of the family of circles in the first quadrant which touch the coordinate axes.
Solution
(x3 - 3xy2)dx = (y3 - 3x2 y)dy
⇒ dy/dx = (x3 - 3xy2)/(y3 - 3x2 y) ...(1)
This is a homogeneous equation. To simplify it, we need to make the substitution as :
y = vx
Substituting the values of y and dy/dx in equation (1), we get :
Integrating both sides, we get :
Substituting the values of I1 and I2 in equation (3), we get :
Therefore, equation (2) becomes:
Hence, the given result is proved.
5. Prove that x2 – y2 = c (x2 + y2)2 is the general solution of differential equation (x3 – 3xy2) dx = (y3 – 3x2y) dy, where c is a parameter.
Solution
The equation of a circle in the first quadrant with centre (a, a) and radius (a) which touches the coordinate axes is :
(x - a)2 + (y - a)2 = a2 ...(1)
Differentiating equation (1) with respect to x, we get :
2(x - a) + 2(y - a) dy/dx = 0
⇒(x - a)+ (y - a)y' = 0
⇒ x - a + yy' - ay' = 0
⇒ x + y y' - a(1 + y') = 0
⇒ a = (x + yy')/(1 + y')
Substituting the value of a in equation (1), we get :
Hence, the required differential equation of the family of circles is
(x - y)2 [1 +(y')2 ] = (x + yy')2.
6. Find the general solution of the differential equation dy/dx + √(1 - y2)/(1 - x2) = 0
Solution

Integrating both sides, we get :
sin-1y = -sin-1x + C
⇒ sin-1x + sin-1y = C

Integrating both sides, we get :

⇒ x + y + 1 = B/√3(1 - xy - 2xy)
⇒ x + y + 1 = A(1 - x - y - 2xy), where A = B/√3
Hence, the given result is proved.
sin x cos y dx + cos x sin ydy = 0
⇒ (sin x cos ydx + cos x sin ydy)/(cos x cos y) = 0
⇒ tan x dx + tan y dy = 0
Integrating both sides, we get :
log (sec x .sec y) = log C
⇒ sec x .sec y = C ...(1)
The curve passes through point (0, π/4).
∴ 1 × √2 = C
⇒ C = √2
sec x . sec y = √2
⇒ sec x . 1/cos y = √2
⇒ cos y = sec x/√2
Hence, the required equation of the curve is cos y = sec x/√2.

⇒ ex = dt/dx
⇒ ex dx = dt
Substituting these values in equation (1), we get :

Now, y = 1 at x = 0.
Therefore, equation (2) becomes:
tan-1 1 + tan-1 1 = C
⇒ π/4 + π/4 = C
⇒ C = π/4
Substituting C = π/4 in equation (2), we get :
tan-1 y + tan-1 (ex) = π/2

Let ex/y = Z
Differentiating it with respect to y, we get :

From equation (1) and equation (2), we get :
dz/dy = 1
⇒ dz = dy
Integrating both sides, we get :
z = y + C
⇒ ex/y = y + C
⇒ (x - y + 1)dy = (1 - x + y)dx

Substituting the values of x - y and dy/dx in equation (1), we get :

Integrating both sides, we get :
t + log |t| = 2x + C
⇒ (x - y) + log |x - y| = 2x + C
⇒ log |x - y| = x + y + C ...(3)
Now, y = -1 at x = 0 . Therefore, equation (3) becomes :
log 1 = 0 - 1 + C
C = 1
Substituting C = 1 in equation (3) we get :
log |x - y| = x + y + 1
This is the required particular solution of the given differential equation.
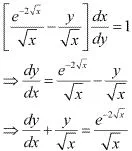
This equation is a linear differential equation of the form
The general solution of the differential equation is given by,

dy/dx + y cot x = 4 x cosec x
The general solution of the given differential equation is given by,
⇒ y sin x = ∫(4x cosec x . sin x)dx + C
⇒ y sin x = 4 ∫x dx + C
⇒ y sin x = 4. x2 /2 + C
⇒ y sin x = 2x2 + C ...(1)
Now, y = 0 at x = π/2
Therefore, equation (1) becomes :
0 = 2 × (π2/4) + C
⇒ C = -(π2/2)
Substituting C = -(π2/2) in equation (1), we get :
y sin x = 2x2 - (π2/2)
This is the required particular solution of the given differential equation.

Substituting this value in equation (1), we get :
⇒ - log |t| = log |C(x + 1)|
⇒ - log |2 - ey| = log |C(x + 1)|

Now, at x = 0 and y = 0, equation (2) becomes :
⇒ 2 - 1 = 1/C
⇒ C = 1
Substituting C = 1 in equation (2), we get :

This is the required particular solution of the given differential equation.

Integrating both sides, we get :
log y + kt + C ...(1)
In the year 1999, t = 0 and y = 20000.
Therefore, we get :
log 20000 = C ...(2)
In the year 2004, t = 5 and y = 25000.
Therefore, we get :
⇒ log 25000 = 5k + log 20000

In the year 2009, t = 10 years.

⇒ y = 20000× 5/4 × 5/4
⇒ y = 31250
Hence, the population of the village in 2009 will be 31250.
(A) xy = C
(B) x = Cy2
(C) y = Cx
(D) y = Cx2

Integrating both sides, we get :
log |x| - log |y| = log k
⇒ log |x/y| = log k
⇒ x/y = k
⇒ y = (1/k)x
⇒ y = Cx where C = 1/x
Hence, the correct answer is C.

The general solution of the differential equation is given by,
Hence, the correct answer is C.
(A xey + x2 = C
(B) xey + y2 = C
(C) yex + x2 = C
(D) yey + x2 = C
ex dy + (yex + 2x)dx = 0
⇒ ex (dy/dx) + yex + 2x = 0
⇒ dy/dx + y = -2xe-x
This is a linear differential equation of the form
The general solution of the given differential equation is given by,
⇒ yex = ∫(-2xe-x .ex) dx + C
⇒ yex = -∫2xdx + C
⇒ yex = -x2 + C
⇒ yex + x2 = C
Hence, the correct answer is C.