NCERT Solutions for Chapter 7 Integrals Class 12 Maths Miscellaneous Exercise

Class 12 Maths NCERT Solutions for Chapter 7 Integrals Miscellaneous Exercise

Integrals Exercise Miscellaneous Solutions

1. Integrate the function 1/(x – x³)

Solution

⇒1 = A(1 - x² ) + Bx(1 + x) + Cx(1 - x) 
⇒ 1 = A - Ax² + Bx + Bx² + Cx - Cx² 
Equating the coefficients of x² , x, and constant term, we obtain 
-A + B - C = 0 
B + C = 0 
A = 1 
On solving these equations, we obtain 

A = 1, B = 1/2, and C = -1/2 
From equation (1), we obtain 

2. Integrate the functions 1/[(√x + a) + √(x + b)]

Solution

3. Integrate the functions 1/x√(ax - x²) [Hint: Put x = a/t]

Solution

4. Integrate the functions 1/[x² (x⁴ + 1)^3/4]

Solution

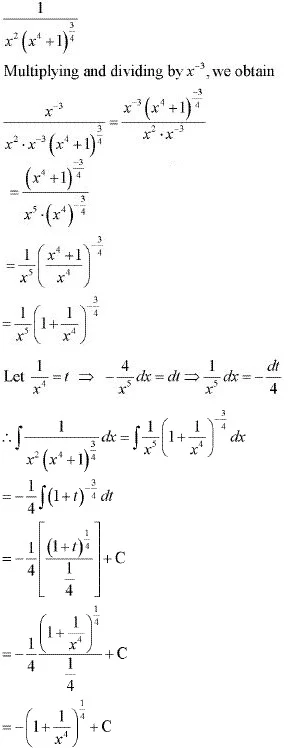
5. Integrate the functions 1/(x^1/2 + x^1/3) [ Hint: 1/(x^1/2 + x^1/3) = 1/[x^1/3 (1 + x^1/6) put x = t⁶] 

Solution

6. Integrate the functions 5x/[(x + 1)(x² + 9)].

Solution

⇒ 5x = A(x² + 9) + (Bx + C)(x + 1) 
⇒ 5x = Ax² + 9A + Bx² + Bx + Cx + C 
Equating the coefficients of x² , x, and constant term, we obtain  
A + B = 0 
B + C = 5 
9A + C = 0 
On solving these equations, we obtain 

a = -1/2, B = 1/2 , and C = 9/2 
From equation (1), we obtain 

7. Integrate the functions sin x/sin(x - a) 

Solution

sin x/sin(x - a) 
Let x - a = t ⇒ dx = dt 

= ∫(cos a + cot t sin a) dt

= t cos a + sin a log |sin t| + C₁ 
= (x - a) cos a + sin a log |sin (x - a)| + C₁ 
= x cos a + sin a log |sin(x - a)| - a cos a + C₁ 
= sin a log |sin(x - a)| + x cos a + C 

8. Integrate the functions (e^{5log x} - e^{4log x})/(e^{3log x} - e^{2log x})

Solution

9. Integrate the functions cos x/√(4 - sin² x) 

Solution

cos x/√(4 - sin² x)
Let sin x = t ⇒ cos x dx = dt 

10. Integrate the functions (sin⁸x - cos⁸x)/(1 - 2sin²x cos²x)

Solution 

11. Integrate the functions 1/[cos(x + a) cos(x + b)] 

Solution

1/[cos(x + a) cos(x + b)] 
Multiplying and dividing by sin(a - b), we obtain 

12. Integrate the functions x³/√(1 - x⁸)

Solution

13. Integrate the functions e^x/[(1 + e^x)(2 + e^x)].

Solution

14. Integrate the functions 1/[(x² + 1)(x² + 4)]

Solution

⇒ 1 = (Ax + B)(x² + 4) + (Cx + D)(x² + 1) 
⇒ 1 = Ax³ + 4Ax + Bx² + 4B + Cx³ + Cx + Dx² + D 

Equating the coefficients of x³ , x² , x, and constant term, we obtain 

A + C = 0 
B + D = 0 
4A + C = 0 
4B + D = 1 
On solving these equations, we obtain 

A = 0, B = 1/3, C = 0, and D = -1/3 
From equation (1), we obtain 

15.  Integrate the functions cos³ xe^{log sinx} 

Solution 

cos³ xe ^{log sinx} = cos³ x × sin x

Let cos x = t ⇒ - sin x dx = dt 

= -∫t³ dt 
= (-t⁴/4) + C 
= (-cos⁴ x/4)  + C

16. Integrate the functions e^{3log x}  (x⁴ + 1)^-1 

Solution

e^{3log x} (x⁴ + 1)^-1 = e^{log x3} (x⁴ + 1)^-1 = x³ /(x⁴ + 1)

Let x⁴ + 1 = t ⇒ 4x³ dx = dt 

⇒ ∫e^{log x} (x⁴ + 1)^-1 dx    

17. Integrate the functions f'(ax + b)[f(ax + b)]ⁿ 

Solution

18. Integrate the functions 1/√[sin³ x sin (x + a)]

Solution

19. Integrate the functions (sin^-1 √x - cos^-1 √x)/(sin^-1√x + cos^-1√x) , x ∊ [0, 1] 

Solution

Let I₁ = ∫cos^-1 √x dx
Also, let √x = t ⇒ dx = 2t dt 
⇒ I₁ = 2∫cos^-1 t.t dt 

20 Integrate the functions √[(1 - √x)/(1 + √x)]

Solution

21. Integrate the functions [(2 + sin 2x)/(1 + cos 2x)] e^x    .

Solution

= ∫(sec² x + tan x)e^x 
let f(x) = tan x ⇒ f'(x) = sec² x 
∴ I = ∫[f(x) + f'(x)]e^x dx 
= e^x f(x) + C 
= e^x tan x + C 

22. Integrate the functions (x² + x + 1)/[(x + 1)² (x +  2)] 

Solution

⇒ x² + x + 1 = A(x + 1)(x + 2) + B(x + 2) + C(x² + 2x + 1)
⇒ x² + x + 1 = A(x² + 3x + 2) + B(x + 2) + C(x² + 2x + 1)
⇒ x² + x + 1 = (A + C)x² + (3A + B + 2C)x + (2A + 2B + C)
Equating the coefficients of x², x, and constant term, we obtain 

A + C = 1 
3A + B + 2C = 1 
2A + 2B + C = 1 
On solving these equations, we obtain 

A = -2, B = 1, and C = 3 
From equation (1), we obtain 

23 Integrate the functions tan^-1 √[(1 - x)/(1 + x)] 

Solution

I =  tan^-1 √[(1 - x)/(1 + x)]  dx 
Let x = cos θ ⇒ dx = - sin θ dθ

= - ∫ tan^-1 tan(θ/2) . sin θ dθ 
= -(1/2)∫ θ. sin θ dθ

= -(1/2)[θ . (- cosθ) - ∫1.(- cosθ)dθ]
= -(1/2)[-θ cos θ + sin θ] 

24. Integrate the functions [√x² + 1{log(x² + 1) - 2 log x}]/x⁴.

Solution

25. Evaluate the definite integrals  ∫_π/2^π  e^x (1 - sin x)/(1 - cos x)] dx

Solution  

26. Evaluate the definite integrals ∫₀^π/4 [(sin x cos x)/(cos⁴ x + sin⁴ x)] dx 

Solution

27. Evaluate the definite integrals ∫₀^π/2 (cos² x dx)/[(x cos² x + 4 sin² x)] 

Solution

28. Evaluate the definite integrals ∫_π/6 ^π/3 [(sin x + cos x)/√(sin2x)] dx 

Solution 

29. Evaluate the definite integrals ∫₀¹ dx/[√(1 + x) - √x] 

Solution

30. Evaluate the definite integrals ∫₀^π/4 [(sin x + cos x)/(9 + 16 sin 2x)] dx 

Solution

Also, let sin x - cos x = t ⇒ (cos x + sin x)dx = dt 
When x = 0, t = -1 and when x = π/4, t = 0 
⇒ (sin x - cos x)² = t² 
⇒ sin² x + cos² x  - 2sin x cos x = t² 
⇒ 1 - sin 2x = t² 
⇒ sin 2x = 1 - t² 

31. Evaluate the definite integrals ∫₀^π/2 sin 2x tan^-1 (sin x) dx 

Solution

Let I =  ∫₀^π/2 sin 2x tan^-1 (sin x) dx =  ∫₀^π/2 2sin x cos x tan^-1 (sin x) dx 
Also, let sin x = t ⇒ cos x dx = dt 
When x = 0, t = 0 and when x = π/2, t = 1 

32. Evaluate the definite integrals ∫₀^π [(x tan x)/(sec x + tan x)] dx 

Solution

Adding (1) and (2), we obtain 

33. Evaluate the definite integrals ∫₁⁴ [|x -1| + |x - 2| + |x - 3|] dx 

Solution

34. Prove the following ∫₁³ dx/[x² (x + 1)] = 2/3 + (log 2)/3 

Solution

⇒ 1 = Ax(x + 1) + B(x + 1) + C(x² )
⇒ 1 = Ax² + Ax + Bx + B + Cx² 
Equating the coefficients of x² , x, and constant term, we obtain 

A + C = 0 
A + B = 0 
B = 1 
On solving these equations, we obtain 

A = -1, C = 1, and B = 1 

= log 4 + log 3 - log 2 + 2/3 
= log 2 - log 3 + 2/3 

= log(2/3) + 2/3 

Hence, the given result is proved. 

35. Prove the following  ∫₀⁴  xe^x dx = 1

Solution

Let I = ∫₀⁴  xe^x dx 
Integrating by parts, we obtain 

= e- e + 1 
= 1 

Hence, the given result is proved . 

36. Prove the following ∫_-1¹ x¹⁷ cos⁴ x dx = 0 

Solution

Let I =  ∫_-1¹ x¹⁷ cos⁴ x dx 
Also, let f(x) = x¹⁷ cos⁴ x 

⇒ f(-x) = (-)¹⁷ cos⁴ (-x) = -x¹⁷ cos⁴ x = - f(x) 
Therefore, f(x) is an odd function. 

It is known that if f(x) is an odd function, then ∫_-1¹  f(x) dx = 0 
∴ I = ∫_-1¹ x¹⁷ cos⁴ x dx = 0 
Hence, the given result is proved. 

37. Prove the following  ∫₀^π/2 sin³ x dx = 2/3 

Solution

Hence, the given result is proved . 

38. Prove the following ∫₀^π/4 2 tan³ x dx = 1 - log 2 

Solution

= 1 - log 2 - log 1 = 1 - log 2 

Hence, the given result is proved. 

39. Prove the following  ∫₀¹ sin^-1 x dx = π/2 - 1 

Solution

Let I = ∫₀¹ sin^-1 x dx
⇒ I = ∫₀¹ sin^-1 x.1. dx 
Integrating by parts, we obtain 

Let 1 - x³ = t ⇒ -2x dx = dt 
When x = 0, t = 1 and when x = 1, t = 0 

Hence, the given result is proved. 

40. Evaluate ∫₀¹ e^2-3x dx as a limit of a sum. 

Solution

Let I = ∫₀¹ e^2-3x dx 
It is known that, 

 Where,  h = (b - a)/n 
Here, a = 0, b = 1, and f(x) = e^2-3x 
⇒ h = (1 - 0)/n = 1/n

41. Choose the correct ∫[dx/(e^x + e - x)] is equal to 

(A) tan^-1 (e^x ) + C 
(B) tan^-1 (e^-x ) + C 
(C) log(e^x - e^-x ) + C 
(D) log(e^x + e^-x ) + C 

Solution

Also, let e^x = t ⇒ e^x dx = dt 
∴ I = ∫[dt/(1 + t² )]

= tan^-1 t + C 
= tan^-1 (e^x ) + C 
Hence, the correct answer is A. 

42. Choose the correct answers ∫[cos 2x/(sin x + cos x)²] dx is equal to 

(A). -1/(sin x + cos x) + C 
(B) log |sin x + cos x| + C 
(C) log |sin x + cos x| + C 
(D) 1/(sin x - cos x)² 

Solution

Let cos x + sin x = t ⇒ ( cos x - sin x)dx = dt 
∴ I = ∫ dt/t 
= log|t| + C 
= log | cos x + sin x| + C 

Hence, the correct answer is B. 

43. Choose the correct answers If f (a + b - x) = f (x), then ∫_a^b x f(x) dx is equal  

Solution

Hence, the correct answer is D. 

44. Choose the correct answer The value of ∫₀¹ tan^-1(2x - 1)/(1 + x - x²) dx is 

(A) 1 
(B) 0 
(C) -1
(D) π/4 

Solution

Adding (1) and (2), we obtain 

2I = ∫₀¹ (tan^-1 x + tan^-1 (1 - x) - tan^-1 (1 - x) - tan^-1 x) dx 
⇒ 2I = 0 
⇒ I = 0 
Hence, the correct answer is B.