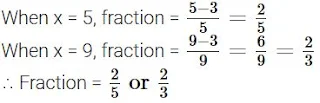Chapter 4 Quadratic Equations Important Questions for CBSE Class 10 Maths Board Exams

Important Questions for Chapter 4 Quadratic Equations Class 10 Maths
Quadratic Equations Class 10 Maths Important Questions Very Short Answer (1 Mark)


Solution
Let one root be α and other root be 6α.

Since k = 0 is not possible, therefore k = 3.
4. If 1 is a root of the equations ay2 + ay + 3 = 0 and y2 + y + b = 0, then find the value of ab.
Solution
ay2 + ay + 3 = 0
⇒ a(1)2 + a(1) + 3 = 0
⇒ 2a = -3
⇒ a = −32
y2 + y + b = 0
⇒ 12 + 1 + b = 0
⇒ b = -2
∴ ab = (−32)(−2) = 3
5. Find the roots of the equation x2 – 3x – m (m + 3) = 0, where m is a constant.
Solution
x2 – 3x – m(m + 3) = 0
⇒ D = b2 – 4ac
⇒ D = (- 3)2 – 4(1) [-m(m + 3)]
= 9 + 4m (m + 3)
= 4m2 + 12m + 9 = (2m + 3)2

∴ x = m + 3 or -m
Quadratic Equations Class 10 Maths Important Questions Short Answer (2 Marks)
6. For what values of k, the roots of the equation x2 + 4x + k = 0 are real?
Solution
Comparing the given equation with ax2 + bx + c = 0, we get a = 1, b = 4, c = k.
Since, given the equation has real roots,
D ≥ 0
⇒ b2 - 4ac ≥ 0
⇒ 42 - 4 × 1 × k ≥ 0
⇒ 4k ≤ 16
⇒ k ≤ 4
7. Find the value of m so that the quadratic equation mx (x – 7) + 49 = 0 has two equal roots.
Solution
We have, mx (x – 7) + 49 = 0
mx2 – 7mx + 49 = 0
Here, a = m, b = – 7m, c = 49
D = b2 – 4ac = 0 …[For equal roots]
⇒ (-7m)2 – 4(m) (49) = 0
⇒ 49m2 – 4m (49) = 0
⇒ 49m (m – 4) = 0
⇒ 49m = 0 or m – 4 = 0
m = 0 (rejected) or m = 4
∴ m = 4
8. Find the value of k for which the roots of the equations 3x2 - 10x + k = 0 are reciprocal of each other.
Solution
Comparing the given equation with ax2 + bx + c = 0 we get a = 3, b = -10, c = k
Let one root be α so other root is 1/α
Now,
product of roots, α × 1/α = c/a
Hence, the value of k is 3.
9. Find the roots of the following quadratic equation :
15x2 - 10√6x + 10 = 0
Solution
We have 15x2 - 10√6x + 10 = 0

Solution
We have, px (x – 3) + 9 = 0
px2 – 3px + 9 = 0 Here a = p, b = -3p,
D = 0
b2 – 4ac = 0
⇒ (-3p)2 – 4(p)(9) = 0
⇒ 9p2 – 36p = 0
⇒ 9p (p – 4) = 0
⇒ 9p = 0 or p – 4= 0
p = 0 (rejected) or p = 4
∴ p = 4 …(∵ Coefficient of x2 cannot be zero)
11. Solve for x:
36x2 – 12ax + (a2 – b2) = 0
Solution
We have, 36x2 – 12ax + (a2 – b2) = 0
⇒ (36x2 – 12ax + a2) – b2 = 0
⇒ [(6x)2 – 2(6x)(a) + (a)2] – b2 = 0
⇒ (6x – a)2 – (b)2 = 0 …[∵ x2 – 2xy + y2 = (x – y)2]
⇒ (6x – a + b) (6x – a – b) = 0 ...[∵ x2 – y2 = (x + y)(x – y)]
⇒ 6x – a + b = 0 or 6x – a – b = 0
⇒ 6x = a – b or 6x = a + b
⇒ x = a− b/6 or a+ b/6
12. Solve for x:
4√3x2 + 5x - 2√3 = 0
Solution
We have, 4√3x2 + 5x - 2√3 = 0
Solution
Here 4x2 + 3x + 5 = 0

But (2x+34)2 cannot be negative for any real value of x.
14. Solve for x : x2 - (√3+1)x + √3 = 0
Solution
x2 - (√3+1)x + √3 = 0
⇒ x2 -√3 x - 1x + √3 = 0
⇒ x(x-√3) - 1(x-√3) = 0
⇒ (x-√3) (x-1) = 0
Thus, x = √3, x = 1
15. Find the roots of the following quadratic equation :
(x+3)(x-1) = 3(x - 1/3)
Solution

Thus x = 2, -1
9x2 - 6b2x - (a4 - b4) = 0
Solution
We have,
9x2 - 6b2x - (a4 - b4) = 0
Comparing with Ax2 + Bx + C
A = 9, B = -6b2, C = -(a4 - b4)


Solution
We have, ax2 + 7x + b = 0
Here ‘a’ = a, ‘b’ = 7, ‘c’ = b
Now, α = 23 and β = -3 …[Given]

Solution
The given quadratic equation can be written as
(9x2 – 6b2x + b4) – a4 = 0
⇒ (3x – b2)2 – (a2)2 = 0
⇒ (3x – b2 + a2) (3x – b2 – a2) = 0 …[x2 – y2 = (x + y) (x – y)]
⇒ 3x – b2 + a2 = 0 or 3x – b2 – a2 = 0
⇒ 3x = b2 – a2 or 3x = b2 + a2

Solution
We have, 2x2 + px – 15 =0
Since (-5) is a root of the given equation
∴ 2(-5)2 + p(-5) – 15 = 0
⇒ 2(25) – 5p – 15 = 0
⇒ 50 – 15 = 5p
⇒ 35 = 5p
⇒ p = 7 …(i)
Now, p(x2 + x) + k
⇒ px2 + px + k = 0
7x2 + 7x + k = 0 …[From (i)]
Here, a = 7, b = 7, c = k
D = 0 …[Roots are equal]
⇒ b2 – 4ac = 0
⇒ (7)2 – 4(7)k = 0 ⇒ 49 – 28k = 0
⇒ 49 = 28k
∴ k = 49/28 = 7/4
13√3 x2 + 10x + √3 = 0
Solution
Given,
13√3 x2 + 10x + √3 = 0
Comparing with ax2 + bx + c = 0, we get
a = 13√3, b = 10, c = √3
b2 - 4ac = 102 - 4(13√3)(√3)
=100 - 156
= -56
As D < 0, the equation has no real roots.
22. Find the positive value of k for which x2 - 8x + k = 0, will have real roots.
Solution
We have,
x2 - 8x + k = 0
Comparing with Ax2 + Bx + C = 0, we get
A = 1, B = -8, C= k
Since the given equation has real roots,
B2 - 4AC > 0
⇒ (-8)2 - 4(1)(k) ≥ 0
⇒ 64 - 4k ≥ 0
⇒ 16 - k ≥ 0
⇒ 16 ≥ k
Thus, k ≤ 16
23. If 2 is a root of the equation x2 + kx + 12 = 0 and the equation x2 + kx + q = 0 has equal roots, find the value of q.
Solution
We have,
x2 + kx + 12 = 0
If 2 is the root of above equation, it must satisfy it.
22 + 2k + 12 = 0
⇒ 2k + 16 = 0
⇒ k = -8
Substituting k = -8 in x2 + kx + q = 0 we have
x2 - 8x + q = 0
For equal roots,
(-8)2 - 4(1)q = 0
⇒ 64 - 4q = 0
⇒ 4q = 64
⇒ q = 16
24. Solve for x : √3 x2 + 10x + 7√3 = 0
Solution

Solution
We have,
2x2 + kx + 8 = 0
Comparing with ax2 + bx + c = 0, we get
a = 2, b = k and c = 8
For equal roots, D = 0,
b2 - 4ac = 0
k2 - 4×2×8 = 0
⇒ k2 = 64
⇒ k = ±√64
Thus k = ±8
Quadratic Equations Class 10 Maths Important Questions Short Answer-II (3 Marks)
26. Find the values of k for which the quadratic equation x2 + 2√2 kx + 18 = 0 has equal roots.
Solution
We have,
x2 + 2√2 kx + 18 = 0
Comparing it by ax2 + bx + c, we get a = 1, b = 2√2 k and c = 18.
Given that,
Equation x2 + 2√2 kx + 18 = 0 has equal roots.
b2 - 4ac = 0
⇒ (2√2 k)2 -4118 = 0
⇒ 8k2 - 72 = 0
⇒ 8k2 = 72
⇒ k2 = 72/8 = 9
⇒ k = ±3
27. If α and β are the zeroes of the polynomial f(x) = x2 - 4x - 5 then find the value of α2 + β2.
Solution
We have,
p(x) = x2 - 4x - 5
Comparing it by ax2 + bx + c, we get a = 1, b = -4 and c = -5.
Since, given α and β are the zeroes of the polynomial,
28. Find the quadratic polynomial, the sum and product of whose zeroes are -3 and 2 respectively. Hence find the zeroes.
Solution
Sum of zeroes,
α + β = -3 ...(1)
and product of zeroes, αβ = 2
Thus quadratic equation is
x2 - (α+β)x + αβ = 0
⇒ x2 - (-3)x + 2 = 0
⇒ x2 + 3x + 2 = 0
Thus quadratic equation is x2 + 3x + 2 = 0
Now, above equation can be written as
x2 + 2x + x + 2 = 0
⇒ x(x+2) + (x+2) = 0
⇒ (x+2) (x+1) = 0
Hence, zeroes are -2 and -1.
29. Find the roots of the following quadratic equation: 2√3 x2 – 5x + √3 = 0
Solution
We have, 2√3 x2 – 5x + √3 = 0
Here, a = 2√3, b = -5, c = √3
D = b2 – 4ac
∴ D = (-5)2 – 4 (2√3)(√3)
= 25 – 24 = 1

Solution
4x2 – 4ax + (a2 – b2) = 0
⇒ [4x2 – 4ax + a2] – b2 = 0
⇒ [(2x)2 – 2(2x)(a) + (a)2] – b2 = 0
⇒ (2x – a)2 – (b)2 = 0
⇒ (2x – a + b) (2x – a – b) = 0
⇒ 2x – a + b = 1 or 2x – a – b = 0
2x = a – b or 2x = a + b
31. Solve for x: 4x2 – 4ax + (a2 – b2) = 0
Solution⇒ [(2x)2 – 2(2x)(a) + (a)2] – b2 = 0
⇒ (2x – a)2 – (b)2 = 0
⇒ (2x – a + b) (2x – a – b) = 0
⇒ 2x – a + b = 1 or 2x – a – b = 0
2x = a – b or 2x = a + b
Solution
Given: 2x2 + kx + 3 = 0
Here a = 2, b = k, c= 3
D = 0 …[Since roots are equal]
As b2 – 4ac = 0
∴ k2 – 4(2)(3) = 0
⇒ k2 – 24 = 0
⇒ k2 = 24
33. Find the value(s) of k so that the quadratic equation 3x2 – 2kx + 12 = 0 has equal roots.
Solution
Given: 3x2 – 2kx + 12 = 0
Here a = 3, b = -2k, c = 12
D = 0 …[Since roots are equal as b2 – 4ac = 0]
∴ (-2k)2 – 4(3) (12) = 0
⇒ 4k2 – 144 = 0
⇒ k2 = 144/4 = 36
∴ k = ±√36
∴ k = ±6
34. Find the quadratic polynomial, the sum and product of whose zeroes are -3 and 2 respectively. Hence find the zeroes.
Solution
Sum of zeroes α + β = -3
and product of zeroes αβ = 2
Thus quadratic equation is
x2 - (α+β)x + αβ = 0
⇒ x2 - (-3)x + 2 = 0
⇒ x2 + 3x + 2 = 0
Thus, quadratic equation is x2 + 3x + 2 = 0
Now, above equation can be written as
x2 + 2x + x + 2 = 0
⇒ x(x+2) + (x+2) = 0
⇒ (x+2) (x+1) = 0
Hence, zeroes are -2 and -1.
35. Find the zeroes of the quadratic polynomial 6x2 - 3 - 7x and verify the relationship between the zeroes and the coefficients.
SolutionWe have,
p(x) = 6x2 - 3 - 7x
For zeroes of polynomial,
p(x) = 0
6x2 - 7x - 3 = 0
⇒ 6x2 - 9x + 2x - 3 = 0
⇒ 3x(2x - 3) + 1(2x-3) = 0
⇒ (2x-3) (3x+1) = 0
Thus, 2x - 3 = 0 and 3x + 1 = 0
Hence, x = 3/2 and x = -1/3
Therefore,
α = 3/2 and β = -1/3 are the zeroes of the given polynomial.
Verification:

6mx2 + 10mx + 25 = 0
Here a = 6m, b = 10m, c = 25
D = 0 …(Since roots are equal)
b2 – 4ac = 0
∴ (10m)2 – 4(6m) (25) = 0
⇒ 100m2 – 600m = 0
⇒ 100m (m – 6) = 0
⇒ 100m = 0 or m – 6 = 0
m = 0 or m = 6 …[Rejecting m = 0, as coefficient of x2 cannot be zero]
∴ m = 6
Solution
We have,
(k + 4) x2 + (k + 1) x + 1 = 0
Here,
a = k + 4, b = k + 1, c = 1
D =0 …[∵ Roots are equal]
b2 – 4ac = 0
∴ (k + 1)2 – 4(k + 4)(1) = 0
k2 + 2k + 1 – 4k – 16 = 0
⇒ k2 – 2k – 15 = 0
⇒ k2 – 5k + 3k – 15 = 0
⇒ k(k – 5) + 3(k – 5) = 0
⇒ (k – 5)(k + 3) = 0
⇒ k – 5 = 0 or k + 3= 0
⇒ k = 5 or k = -3
∴ k = 5 and -3
38. Find the zeroes of the quadratic polynomial x2 + 7x + 10, and verify the relationship between the zeroes and the coefficients.
Solution
Let
p(x) = x2 + 7x + 10
For zeroes of polynomial p(x) = 0,
x2 + 7x + 10 = 0
⇒ x2 + 5x + 2x + 10 = 0
⇒ x(x+5) + 2(x+5) = 0
⇒ (x+5) (X+2) = 0
So,
x = -2 and x = -5
Therefore, α = -2 and β = -5 are the zeroes of the given polynomial.
Verification:
Sum of zeroes,
α + β = -2 + (-5)


Solution
y2 + k2 = 2(k + 1)y
y2 – 2(k + 1)y + k2 = 0
Here a = 1, b = -2(k + 1), c = k2
D = 0 …[Roots are equal]
b2 – 4ac = 0
∴ [-2(k + 1)]2 – 4 × (1) × (k2) = 0
⇒ 4(k2 + 2k + 1) – 4k2 = 0
⇒ 4k2 + 8k + 4 – 4k2 = 0
⇒ 8k + 4 = 0
⇒ 8k = -4
∴ k = -4/8 = -1/2
41. Solve the equation 3/x+1 - 1/2 = 2/3x-1, x≠ -1, x≠ 1/3 for x.
Solution
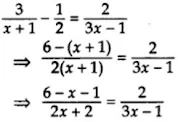
⇒ 2(2x + 2) = (5 – x)(3x – 1)
⇒ 4x + 4 = 15x – 5 – 3x2 + x
⇒ 4x + 4 – 15x + 5 + 3x2 – x = 0
⇒ 3x2 – 12x + 9 = 0
⇒ x2 – 4x + 3 = 0 …[Dividing by 3]
⇒ x2 – 3x – x + 3 = 0
⇒ x(x – 3) – 1(x – 3) = 0
⇒ (x – 1) (x – 3) = 0
⇒ x – 1 = 0 or x – 3 = 0
∴ x = 1 or x = 3
42. Solve for x:
2x/x-3 + 1/2x+3 + 3x+9/(x+9)(2x+3) = 0, x ≠ 3, -3/2
Solution
2x(2x+3) + (x-3) + (3x+9) = 0
⇒ 4x2 + 6x + x - 3 + 3x + 9 = 0
⇒ 4x2 + 10x + 6 = 0
⇒ 2x2 + 5x + 3 =0
⇒ (x+1) (2x+3) = 0
Thus, x = -1, x = -3/2
43. Solve the following quadratic equation for x :
x22 + (a/a+b + a+b/a)x + 1 = 0
Solution


Solution
We have,
x2 - (2b-1)x + (b2-b-20) = 0
Comparing with Ax2 + Bx + C = 0 we have
A = 1, B = -(2b-1), C = (b2-b-20)

Thus x = b+4 and x = b-5
46. Find the roots of the equation 2x2 + x - 4 = 0, by the method of completing the squares.
Solution
We have,
2x2 + x - 4 = 0

Solution
Let three consecutive natural numbers are x, x + 1, x + 2.
According to the question,
(x + 1)2 – [(x + 2)2 – x2] = 60
⇒ x2 + 2x + 1 – (x2 + 4x + 4 – x2) = 60
⇒ x2 + 2x + 1 – 4x – 4 – 60 = 0
⇒ x2 – 2x – 63 = 0
⇒ x2 – 9x + 7x – 63 = 0
⇒ x(x – 9) + 7(x – 9) = 0
⇒ (x – 9) (x + 7) = 0
⇒ x – 9 = 0 or x + 7 = 0
⇒ x = 9 or x = -7
Natural nos. can not be negative, ∴ x = 9
∴ Numbers are 9, 10, 11.
48. If the sum of two natural numbers is 8 and their product is 15, find the numbers.
Solution
Let the numbers be x and (8 – x).
According to the Question,
x(8 – x) = 15
⇒ 8x – x2 = 15
⇒ 0 = x2 – 8x + 15
⇒ x2 – 5x – 3x + 15 = 0
⇒ x(x – 5) – 3(x – 5) = 0
⇒ (x – 3)(x – 5) = 0
x – 3 = 0 or x – 5 = 0
x = 3 or x = 5
When x = 3, numbers are 3 and 5.
When x = 5, numbers are 5 and 3.
49. If 2 is a root of the quadratic equation 3x2 + px - 8 = 0 and the quadratic equation 4x2 - 2px + k = 0 has equal roots, find k.
Solution
We have,
3x2 + px - 8 = 0
Since 2 is a root of above equation, it must satisfy it.
Substituting, x= 2 in we have
12 + 2p - 8 = 0
⇒ p = -2
Since,
4x2 - 2px + k = 0 has equal roots.
or, 4x2 + 4x + k = 0 has equal roots.
D = b2 - 4ac = 0
42 - 4(4)(k) = 0
⇒ 16 - 16k = 0
⇒ 16k = 16
⇒ k = 1
50. If -3 is a root of quadratic equation 2x2 + px - 15 = 0, while the quadratic equation x2 - 4px + k = 0 has equal roots. Find the value of k.
Solution
Given -3 is a root of quadratic equation.
We have,
2x2 + px - 15
Since 3 is a root of above equation, it must satisfy it.
Substituting x 3 = in above equation we have,
2(-3)2 + p(-3) - 15 = 0
⇒ 2×9 - 3p - 15 = 0
⇒ p = 1
Since,
x2 - 4px + k = 0 has equal roots
or, x2 - 4x + k = 0 has equal roots.
b2 - 4ac = 0
⇒ (-4)2 - k = 0
⇒ 16 - 4k = 0
⇒ 4k = 16
⇒ k = 4
51. Solve 1/(a+b+x) = 1/a + 1/b + 1/x, a+b ≠ 0
Solution
We have,

Quadratic Equations Class 10 Maths Important Questions Long Answer (4 Marks)
Solution

⇒ 2x = -8x + 40
⇒ 10x = 40
⇒ x = 4
Hence, x = 15, 4
53. Solve for x: 1/x+1 + 2/x+2 = 4/x+4, x≠ -1,-2,-4
Solution


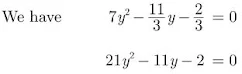
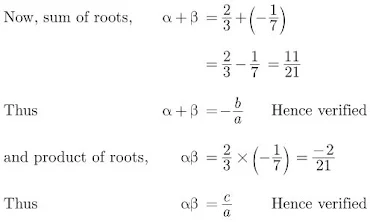
Solution
(3k + 1)x2 + 2(k + 1) + 1 = 0
Here, a = 3k + 1, b = 2(k + 1), c = 1
D = 0 …[∵ Roots are equal]
As b2 – 4ac = 0
∴ [2(k + 1)]2 – 4(3k + 1)(1) = 0
⇒ 4(k + 1)2 – 4(3k + 1) = 0
⇒ 4(k2 + 2k + 1 – 3k – 1) = 0
⇒ (k2 – k) = 0/4
⇒ k(k – 1) = 0
⇒ k = 0 or k – 1 = 0
∴ k = 0 or k = 1
Roots are x = −b/2a ...[ Given, equal roots]

Solution
(2p + 1)x2 – (7p + 2)x + (7p – 3) = 0
Here, a = 2p + 1, b = -(7p + 2), c = 7p – 3
D = 0 …[∵ Equal roots As h2 – 4ac = 0]
∴ [-(7p + 2)]2 – 4(2p + 1)(7p – 3) = 0
⇒ (7p + 2)2 – 4(14p2 – 6p + 7p – 3) = 0
⇒ 49p2 + 28p + 4 – 56p2 + 24p – 28p + 12 = 0
⇒ -7p2 + 24p + 16 = 0
⇒ 7p2 – 24p – 16 = 0 …[Dividing both sides by -1]
⇒ 7p2 – 28p + 4p – 16 = 0
⇒ 7p(p – 4) + 4(p – 4) = 0
⇒ (p – 4) (7p + 4) = 0
⇒ p – 4 = 0 or 7p + 4 = 0
⇒ p = 4 or p = −4/7


59. Check whether the equation 5x2 - 6x - 2 = 0 has real roots if it has, find them by the method of completing the square. Also verify that roots obtained satisfy the given equation.
Solution
We have,
5x2 - 6x - 2 = 0
Comparing with ax2 + bx + c = 0 we get,
a = 5, b = -6 and c = -2
b2 - 4ac = (-6)2 - 4×5×(-2)
= 36 + 40 = 76 > 0
So the equation has real and two distinct roots.
5x2 - 6x = 2
Dividing both the sides by 5 we get

Solution
Let the number of books he bought = x
Increased number of books he had bought = x +4
Total amount = ₹80
According to the problem,
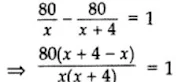
⇒ x(x + 4) = 320
⇒ x2 + 4x – 320 = 0
⇒ x2 + 20x – 16x – 320 = 0
⇒ x(x + 20) – 16(x + 20) = 0
⇒ (x + 20) (x – 16) = 0
⇒ x + 20 = 0 or x – 16 = 0
⇒ x = -20 …(neglected) or x = 16
∴ Number of books he bought = 16
62. Find the positive values of k for which quadratic equations x2 + kx + 64 = 0 and x2 - 8x + k = 0 both will have the real roots.
Solution
(i) For x2 + kx + 64 = 0 to have real roots
k2 - 256 ≥ 0
⇒ k2 ≥ 256
⇒ k ≥ 16 or k < -16
(ii) For x2 - 8x + k = 0 to have real roots
64 - 4k ≥ 0
⇒ 16 - k ≥ 0
⇒ 16 ≥ k
Therefore, For (i) and (ii) to hold simultaneously
k = 16
63. Sum of the areas of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of the two squares.
Solution
Let the side of Large square = x cm
Let the side of small square = y cm
According to the Question,
x2 + y2 = 400 …(i) …[∵ area of square = (side)2]
4x – 4y = 16 …[∵ Perimeter of square = 4 sides]
⇒ x – y = 4 …[Dividing both sides by 4]
⇒ x = 4 + y …(ii)
Putting the value of x in equation (i),
(4 + y)2 + y22 = 400
⇒ y2 + 8y + 16 + y2 – 400 = 0
⇒ 2y2 + 8y – 384 = 0
⇒ y2 + 4y – 192 = 0 …[Dividing both sides by 2]
⇒ y2 + 16y – 12y – 192 = 0
⇒ y(y + 16) – 12(y + 16) = 0
⇒ (y – 12)(y + 16) = 0
⇒ y – 12 = 0 or y + 16 = 0
⇒ y = 12 or y = -16 …[Neglecting negative value]
∴ Side of small square = y = 12 cm and Side of large square = x = 4 + 12 = 16 cm
64. The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
Solution
Let the length of shorter side be x m.
∴ length of diagonal = (x + 16) m
and length of longer side = (x + 14) m
Using pythagoras theorem,
(l)2 + (b)2 = (h)2
∴ x2 + (x + 14)22 = (x + 16)2
⇒ x2 + x2 + 196 + 28x = x2 + 256 + 32x
⇒ x2 – 4x – 60 = 0
⇒ x2 – 10x + 6x – 60 = 0
⇒ x(x – 10) + 6(x – 10) = 0
⇒ (x – 10) (x + 6) = 0
⇒ x – 10 = 0 or x + 6 = 0
⇒ x = 10 or x = -6 (Neglect as length cannot be negative])
⇒ x = 10 m
Length of shorter side = x = 10 m
Length of diagonal = (x + 16) m = 26 m
Length of longer side = (x + 14)m = 24m
∴ Length of sides are 10 m and 24 m.
65. The sum of two numbers is 9 and the sum of their reciprocals is 1/2. Find the numbers.
Solution
Let the numbers be x and 9 – x.
According to the Question,

⇒ 18 = 9x – x2
⇒ x2 – 9x + 18 = 0
⇒ x2 – 3x – 6x + 18 = 0
⇒ x(x – 3) – 6(x – 3) = 0
⇒ (x – 3) (x – 6) = 0
⇒ x – 3 = 0 or x – 6 = 0
⇒ x = 3 or x = 6
When x = 3, numbers are 3 and 6.
When x = 6, numbers. are 6 and 3.
66. Find the nature of the roots of the quadratic equation 4x2 + 4√3x + 3 = 0.
Solution
Given,
4x2 + 4√3x + 3 = 0
Comparing the given equation with ax2 + bx + c = 0, we get
a = 4, b = 4√3 and c = 3.

Since, b2 - 4ac = 0, then roots of the given equation are real and equal.
67. The sum of three numbers in A.P. is 12 and sum of their cubes is 288. Find the numbers.
Solution
Let three numbers in A.P. are a – d, a, a + d.
a – d + a + a + d = 12
⇒ 3a = 12
⇒ a = 4
(a – d)3 + (a)3 + (a + d)3 = 288
⇒ a3 – 3a2d + 3ad2 – d3 + a3 + a3 + 3a2d + 3ad2 + d3 = 288
⇒ 3a3 + 6ad2 = 288
⇒ 3a(a2 + 2d2) = 288
⇒ 3 × 4(42 + 2d2) = 288
⇒ (16 + 2d2) = 288/12
⇒ 2d2 = 24 – 16 = 8
⇒ d2 = 4
⇒ d = ± 2
When, a = 4, d = 2, numbers are:
a – d, a, a + d, i.e., 2, 4, 6
When, a = 4, d = -2, numbers are:
a – d, a, a + d, i.e., 6, 4, 2
68. Find the values of k for which the quadratic equations (k+4)x2 + (k+1)x + 1 = 0 has equal roots. Also, find the roots.
Solution
Given,
(k+4)x2 + (k+1)x + 1 = 0
Comparing with Ax2 + Bx + C = 0, we get
A = (k+4), B = (k+1), C = 1
If roots are equal, B2 - 4AC = 0
(k+1)2 - 4(k+4)(1) = 0
⇒ k2 + 1 + 2k - 4k - 16 = 0
⇒ k2 - 2k -15 = 0
⇒ (k-5) (k+3) = 0
⇒ k = 5, -3
For k = 5, equation becomes
9x2 + 6x + 1 = 0
⇒ (3x+1)2 = 0
⇒ x = -1/3
For k = -3, equation becomes
x2 - 2x + 1 = 0
⇒ (x-1)2 = 0
⇒ x = 1
Hence, roots are 1 and -1/3
69. The perimeter of a right triangle is 60 cm. Its hypotenuse is 25 cm. Find the area of the triangle.
Solution

Perimeter of right ∆ = 60 cm …[Given]
a + b + c = 60
⇒ a + b + 25 = 60
⇒ a + b = 60 – 25 = 35 …(i)
In rt. ∆ACB, AC2 + BC2 = AB2
b2 + a2 = (25)2 …[Pythagoras’ theorem]
⇒ a2 + b2 = 625 …(ii)
From (i), a + b = 35
(a + b)2 = (35) …[Squaring both sides]
⇒ a2 + b2 + 2ab = 1225
⇒ 625 + 2ab = 1225 …[From (ii)]
⇒ 2ab = 1225 – 625 = 600
⇒ ab = 300 …(iii)
Area of ∆ = 1/2 × base × corresponding altitude
= 1/2 × b × a = 1/2 (300) ...[From (iii)]
= 150 cm2
70. The numerator of a fraction is 3 less than its denominator. If 1 is added to the denominator, the fraction is decreased by 1/15. Find the fraction.
Solution
Let the denominator be x and the numerator be x – 3.
∴ Fraction =x−3/x
New denominator = x + 1
According to the Question,
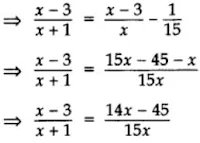
⇒ 15x2 – 45x = 14x2 – 45x + 14x – 45
⇒ 15x2 – 14x2 – 14x + 45 = 0
⇒ x2 – 14x + 45 = 0
⇒ x2 – 5x – 9x + 45 = 0
⇒ x(x – 5) – 9(x – 5) = 0
⇒ (x – 5) (x – 9) = 0
⇒ x – 5 = 0 or x – 9 = 0
⇒ x = 5 or x = 9