NCERT Solutions for Class 12th: Ch 2 Inverse Trigonometric Functions Miscellaneous Exercise Math
Page No: 51
Miscellaneous Exercise on Chapter 2
Find the value of the following:
Question: 1

Answer

Question: 2

Answer

Prove that
Question: 3

Answer
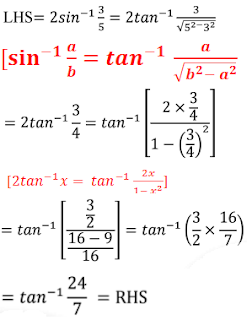
Question: 4

Answer

Question: 5

Answer

Question: 6
Answer

Question: 7
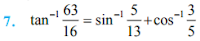

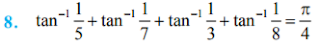




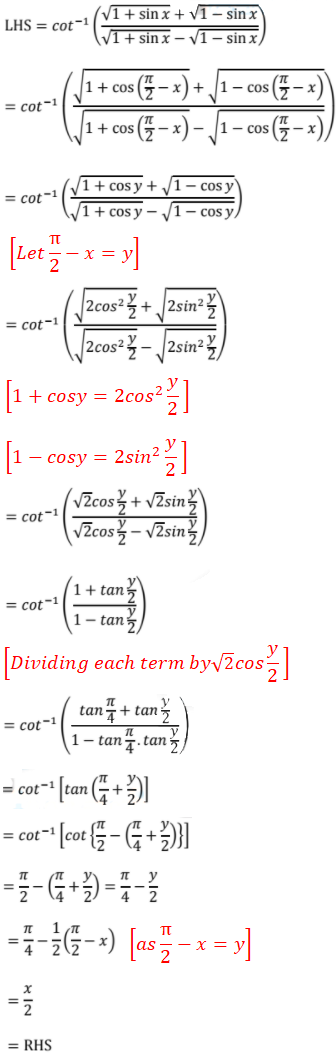

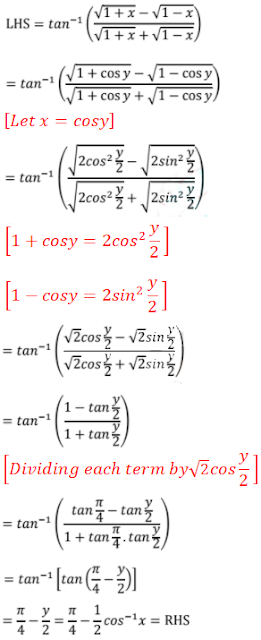







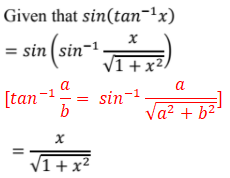

Exercise 2.1 Inverse Trigonometry
Answer

Question: 8
Answer

Page No. 52
Prove that
Question: 9

Answer

Question: 10

Answer
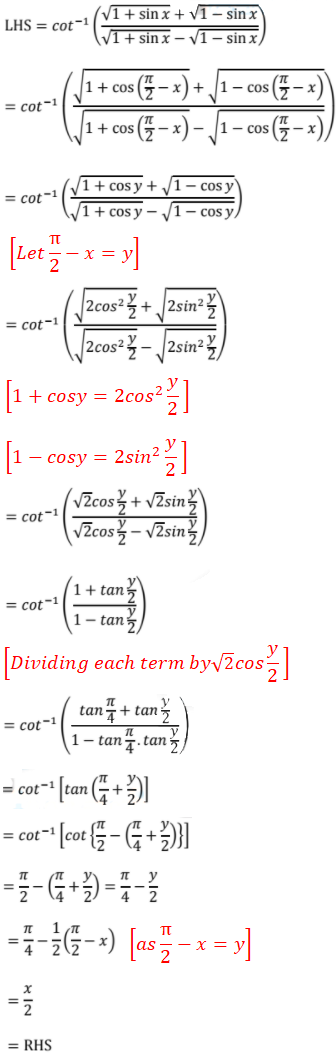
Question: 11

Answer
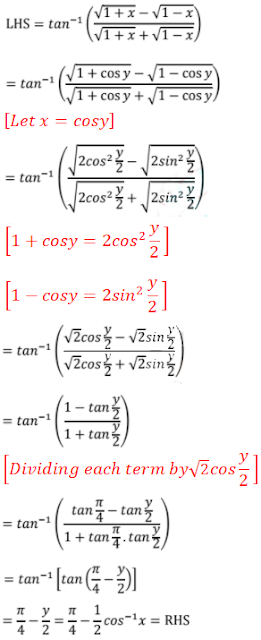
Question: 12
Answer

Solve the following equations:
Question: 13

Answer

Question: 14
Answer

Question: 15

Answer
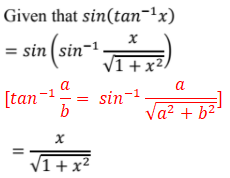
The correct option is D.
Question: 16
sin–1(1 – x) – 2 sin–1x = π/2, then x is equal to
(A) 0, 1/2
(B) 1, 1/2
(C) 0
(D) 1/2
Answer
Given that sin–1(1 − x) − 2sin–1x = π/2
Let x = sin y
∴ sin–1(1 − sin y) − 2y = π/2
⇒ sin–1(1 − sin y) = π/2 + 2y
⇒ 1 − sin y = sin (π/2 + 2y)
⇒ 1 − sin y = cos 2y
⇒ 1 − sin y = 1 − 2sin2y [as cos2y = 1−2sin2y]
⇒ 2sin2y − sin y = 0
⇒ 2x2 − x = 0 [as x = sin y]
⇒ x(2x − 1) = 0
⇒ x = 0 or, x = 1/2
But x = 1/2 does not satisfy the given equation.
∴ x = 0 is the solution of the given equation.
The correct option is C.
Question: 17
tan–1(x/y) − tan–1(x-y/x+y) is equal to
(A) π/2
(B) π/3
(C) π/4
(D) -3π/4
Answer

The correct option is C.
