Class 9 Maths Chapter 10 Circles 10.6 NCERT Solutions in Hindi Medium

वृत्त Ganit NCERT Solutions in Hindi Medium Exercise 10.6
प्रश्न 1. सिद्ध कीजिए कि दो प्रतिच्छेद करते हुए वृत्तों को केन्द्रों की रेखा दोनों प्रतिच्छेद बिन्दुओं पर समान कोण आन्तरित करती है।
Solution
दिया है: केन्द्रों O तथा O' के साथ दो वृत्त हैं जो परस्पर एक-दूसरे को C तथा D पर प्रतिच्छेद करते हैं।
सिद्ध करना है: ∠OCO' = ∠ODO'
रचना: OC, OD, O'C तथा O'D को मिलाते हैं।

प्रमाण:
∆OCO' तथा ∆ODO' में,
OC = OD (एक वृत्त की त्रिज्या)
O'C = O'D (एक वृत्त की त्रिज्या)
OO' = OO′ (उभयनिष्ठ)
SSS युक्ति से,
∆OCO' = ∆ODO'
अतः ∠OCO' = ∠ODO' (CPCT द्वारा)
प्रश्न 2. एक वृत्त की 5 सेमी तथा 11 सेमी लम्बी दो जीवाएँ AB और CD समान्तर हैं और केन्द्र की विपरीत दिशा में स्थित हैं। यदि AB और CD के बीच की दूरी 6 सेमी हो, तो वृत्त की त्रिज्या ज्ञात कीजिए |
Solution
माना दिए गए वृत्त का केन्द्र O है तथा इसकी त्रिज्या b सेमी है। ON ⟂ AB तथा OM ⟂ CD खींचते हैं।
चूँकि ON ⟂ AB, OM ⊥CD तथा AB || CD, अतः बिन्दुओं N, O, M संरेखीय हैं।

माना, ON = a सेमी
∴ OM = (6 – a) सेमी
OA तथा OC मिलाते हैं।
तब, OA = OC = b सेमी
चूँकि, वृत्त के केन्द्र से एक जीवा पर डाला गया लम्ब जीवा को समद्विभाजित करता है।
अतः AN = NB = 2.5 सेमी तथा OM = MD = 5.5 सेमी
∆OAN तथा ∆OCM में,
OA2 = ON2 + AN2
तथा OC2 = OM2 + CM2
⇒ b2 = a2 + (2.5)2
तथा b2 = (6 – a)2 + (5.5)2 ...(i)
अतः a2 + (2.5)2 = (6 - a)2 + (5.5)2
⇒ a2 + 6.25 = 36 - 12a + a2 + 30.25
⇒ 12a = 60
⇒ a = 5
a = 5 समी (i) में रखने पर,
b2 = (5)2 + (2.5)2 = 25 + 6.25 = 31.25

प्रश्न 3. किसी वृत्त की दो समान्तर जीवाओं की लम्बाइयाँ 6 सेमी और 8 सेमी हैं । यदि छोटी जीवा केन्द्र से 4 सेमी की दूरी पर हो, तो दूसरी जीवा केन्द्र से कितनी दूर है ?
Solution
माना केन्द्र O के साथ एक वृत्त की दो समान्तर जीवाएँ PQ तथा RS इस प्रकार हैं कि PQ = 6 सेमी तथा RS = 8 सेमी।
माना वृत्त की त्रिज्या a सेमी है।

ON ⊥ RS, OM ⊥ OQ खींचते हैं।
चूँकि PQ || RS तथा ON ⊥ RS, OM ⊥ PQ।
इस प्रकार बिन्दु O, N तथा M संरेखीय हैं।
∵ OM = 4 सेमी तथा PQ और RS के मध्य-बिन्दु क्रमश: M तथा N हैं।
∆OPM में,
OP2 = OM2 + PM2
⇒ a2 = 42 + 32 = 16 + 9 = 25
⇒ a = 5
∆ORN में,
OR2 = ON2 + RN2
⇒ a2 = ON2 + (4)2
⇒ 25 = ON2 + 16
⇒ ON2 = 9
⇒ ON = 3 सेमी
अतः केन्द्र से जीवा RS की दूरी 3 सेमी है।
प्रश्न 4. मान लीजिए कि ∠ABC का शीर्ष एक वृत्त के बाहर स्थित है और कोण की भुजाएँ वृत्त से बराबर जीवाएँ AD तथा CE काटती हैं। सिद्ध कीजिए कि ∠ABC जीवाओं AC तथा DE द्वारा केन्द्र पर आन्तरित कोणों के अन्तर का आधा है।
Solution
चूँकि एक त्रिभुज का बाह्य कोण सम्मुख अन्तः कोणों के योग के बराबर होता है।

∴ ∆BDC में,
∠ADC = ∠DBC + ∠DCB ...(i)
चूँकि एक चाप द्वारा केन्द्र पर आन्तरित कोण वृत्त के शेष भाग के किसी बिन्दु पर आन्तरित कोण का दोगुना होता है।
अतः ∠ABC जीवाओं AC तथा DE द्वारा केन्द्र पर आन्तरित कोणों के अन्तर का आधा है।
प्रश्न 5. सिद्ध कीजिए कि किसी समचतुर्भुज की किसी भुजा को व्यास मानकर खींचा गया वृत्त उसके विकर्णों के प्रतिच्छेद बिन्दु से होकर जाता है।
Solution
दिया है: PQRS एक समचतुर्भुज है। PR तथा SQ इसके दो विकर्ण हैं जो परस्पर एक-दूसरे को समकोण पर प्रतिच्छेदित करते हैं।
सिद्ध करना है: PQ को व्यास मानकर खींचा गया वृत्त 0 से होकर जाता है।
रचना: O से होकर MN || PS तथा EF || PQ खींचते हैं।

प्रमाण:
∵ PQ = SR ⇒ ½PQ = ½SR
अतः PN = SM
इसी प्रकार, PE = ON
अतः PN = ON = NQ
इस प्रकार, केन्द्र N तथा त्रिज्या PN के साथ एक वृत्त खींचा जाता है जो बिन्दु P, O, Q से होकर गुजरता है।
प्रश्न 6. ABCD एक समान्तर चतुर्भुज है। A, B और C से जाने वाला वृत्त CD (यदि आवश्यक हो तो बढ़ाकर) को E पर प्रतिच्छेद करता है । सिद्ध कीजिए कि AE = AD है।
Solution
चूँकि ABCE एक चक्रीय चतुर्भुज है। इस प्रकार
∠AED + ∠ABC = 180° ...(i)
(∵ एक चक्रीय चतुर्भुज के सम्मुख कोणों का योग 180° होता है)

अतः ∠ADE + ∠ABC = 180° ...(ii)
(∵ ∠ADC = ∠ABC, समान्तर चतुर्भुज के सम्मुख कोण)
समी (i) तथा (ii) से,
∠AED + ∠ABC = ∠ADE + ∠ABC
⇒ ∠AED = ∠ADE
∵ ∆AED में,
∠AED = ∠ADE
अतः AD = AE (∵ एक त्रिभुज में समान कोणों की सम्मुख भुजाएँ समान होती हैं)
प्रश्न 7. AC और BD एक वृत्त की जीवाएँ हैं जो परस्पर समद्विभाजित करती हैं। सिद्ध कीजिए:
(i) AC और BD व्यास हैं
(ii) ABCD एक आयत है।
Solution
(i) माना AB तथा AC एक वृत्त की दो जीवाएँ हैं जो परस्पर एक-दूसरे को P पर प्रतिच्छेद करती हैं।

∆APB तथा ∆CPD में,
PA = PC (∵ AC का मध्य- बिन्दु P है)
∠APB = ∠CPD (शीर्षाभिमुख कोण)
तथा PB = PD (∵ BD का मध्य-बिन्दु P है)
∴ SAS युक्ति द्वारा,
इसलिए BD वृत्त को दो बराबर भागों में विभाजित करती है। अतः BD एक व्यास है। इसी प्रकार, AC एक व्यास है।
(ii) अब, BD तथा AC परस्पर एक-दूसरे को समद्विभाजित करते हैं। अत: ABCD एक समान्तर चतुर्भुज है।
तथा AC = BD
अत: ABCD एक आयत है।
प्रश्न 8. एक ∆ABC के ∠A, ∠B और ∠C के समद्विभाजक इसके परिवृत्त को क्रमशः D, E और F पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि ∆DEF के कोण 90° - ½ A, 90° - ½ B तथा 90°- ½ C हैं।
Solution
∵ ∠EDF = ∠EDA + ∠ADF ...(i)
∵∠EDA तथा ∠EBA एक ही वृत्तखण्ड के कोण हैं।

∴ ∠EDA = ∠EBA
तथा इसी प्रकार, ∠ADF तथा ∠FCA एक ही वृत्तखण्ड के कोण हैं।
अतः ∠ADF = ∠FCA
समी (i) से,
प्रश्न 9. दो सर्वांगसम वृत्त परस्पर बिन्दुओं A और B पर प्रतिच्छेद करते हैं। A से होकर कोई रेखाखण्ड PAQ इस प्रकार खींचा गया है कि P और Q दोनों वृत्तों पर स्थित हैं । सिद्ध कीजिए कि BP = BQ है।
Solution
माना O' तथा O दो सर्वांगसम वृत्तों के केन्द्र हैं।
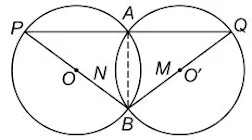
चूँकि इन वृत्तों की एक उभयनिष्ठ जीवा AB है।
∴ ∠BPA = ∠BQA
(चूँकि समान जीवाओं द्वारा आन्तरित कोण भी समान होते हैं)
⇒ BP = BQ
प्रश्न 10. किसी ABC में, यदि ∠A का समद्विभाजक तथा BC का लम्ब समद्विभाजक प्रतिच्छेद करे, तो सिद्ध कीजिए कि वे ∆ABC के परिवृत्त पर प्रतिच्छेद करेंगे।
Solution
(i) माना ∠A का समद्विभाजक ∆ABC के परिवृत्त को M पर मिलता है।
BM तथा CM को मिलाते हैं।

∴ ∠MBC = ∠MAC (एक ही वृत्तखण्ड के कोण हैं)
तथा ∠BCM = ∠BAM (एक ही वृत्तखण्ड के कोण हैं)परन्तु ∠BAM = ∠CAM (∵ ∠A का समद्विभाजक AM है) ...(i)
∴ ∠MBC = ∠BCM
अतः MB = MC (समान कोणों की सम्मुख भुजाएँ भी समान होती हैं)
अत: M, BC के लम्बार्द्धक पर जरुर स्थित होगा।
(ii) माना BC के लम्बार्द्धक पर बिन्दु M है जो ∆ABC के परिवृत्त पर स्थित है। AM को मिलाते हैं।
चूँकि BC के लम्बार्द्धक पर M स्थित है।
∴ BM = CM
∠MBC = ∠MCB
परन्तु ∠MBC = ∠MAC (एक ही वृत्तखण्ड के कोण हैं)
तथा ∠MCB = ∠BAM (एक ही वृत्तखण्ड के कोण हैं)
अतः समी (i) से,
∠BAM = ∠CAM
∠A का समद्विभाजक AM है।
अतः ∠A का समद्विभाजक तथा BC का लम्ब समद्विभाजक ∆ABC के परिवृत्त पर बिन्दु M पर मिलते हैं।




