Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles 9.3 NCERT Solutions in Hindi Medium

समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ganit NCERT Solutions in Hindi Medium Exercise 9.3
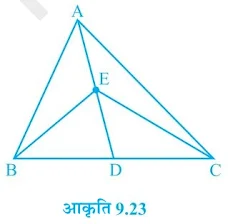
प्रश्न 1. आकृति 9.23 में, ΔABC की एक मध्यिका AD पर स्थित E कोई बिंदु है | दर्शाइए कि ar(ABE) = ar(ACE) है |
Solution
दिया है, AD, ΔABC की एक माध्यिका है तथा AD पर कोई बिन्दु E स्थित है।
चूँकि AD, ΔABC की माध्यिका है।
∴ ar (ΔABD) = ar (ΔACD) ...(i) [∵ त्रिभुज की एक माध्यिका इसको बराबर क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है। तथा ΔEBC की माध्यिका ED है।]
∴ ar (ABED) = ar (ACED) ...(ii)
समी (i) में से समी (ii) को घटाने पर,
ar (ΔABD) - ar (ΔBED) = ar (ΔACD) - ar (ΔCED)
⇒ ar (ΔABE) = ar (ΔACE)
प्रश्न 2. आकृति 9.24 में, ΔABC में, E मध्यिका AD का मध्य-बिंदु है | दर्शाइए कि:
ar (BED) = 1/4 ar(ABC) है |
Solution

दिया है, ΔABC में, E माध्यिका AD का मध्य- बिन्दु है।
हम जानते हैं कि, एक त्रिभुज की माध्यिका इसको बराबर क्षेत्रफल वाले दो त्रिभुजों में बाँटती है।
∴ ar (ΔABD) = ar (ΔADC)
या, ar (ΔABD) = 1/2 ar (ΔABC) ...(i)
ΔABD में, BE एक माध्यिका है।
∴ ar(ΔBED) = ar (ΔBAE) ...(ii)

प्रश्न 3. दर्शाइए कि समांतर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।
Solution
दिया है, समान्तर चतुर्भुज ABCD में इसके विकर्ण AC तथा BD बिन्दु O पर प्रतिच्छेद करते हैं।
हमें सिद्ध करना है कि समान्तर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।
अर्थात् ar (ΔOAB) = ar (ΔOBC) = ar (ΔOCD) = ar (ΔOAD)

हम जानते हैं कि, समान्तर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं। अतः
OA = OC तथा OB = OD
तथा एक त्रिभुज की माध्यिका इसे दो बराबर क्षेत्रफलों वाले त्रिभुजों में बाँटती है।
अतः ΔABC में, BO माध्यिका है।
∴ ar (ΔOAB) = ar (ΔOBC) ...(i)
तथा ΔABD में, AO माध्यिका है।
∴ ar (ΔOAB) = ar (ΔOAD) ...(ii)
इसी प्रकार, ΔACD में, DO माध्यिका है।
∴ ar (ΔOAD) = ar (ΔOCD) ...(iii)
समी (i), (ii) तथा (iii) से,
ar (ΔOAB) = ar (ΔOBC) = ar (ΔOCD) = ar (ΔOAD)
प्रश्न 4. आकृति 9.24 में, ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं | यदि रेखाखंड CD रेखाखंड AB से बिंदु O पर समद्विभाजित होता है, तो दर्शाइए कि ar(ABC) = ar(ABD)
Solution
दिया है, समान आधार AB पर दो ΔABC तथा ΔABD स्थित हैं। AB द्वारा रेखाखण्ड CD बिन्दु पर समद्विभाजित होता है। (∵ OC = OD)
ΔACD में,
OC = OD (दिया है)
अतः AO माध्यिका है।
चूँकि एक त्रिभुज की माध्यिका इसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।
∴ ar (ΔAOC) = ar (ΔAOD) ...(i)
इसी प्रकार, ΔBCD में, ar(BOC) = ar(BOD) ...(ii)
समी (i) तथा (ii) को जोड़ने पर,
ar (ΔAOC) + ar (ΔBOC) = ar (ΔAOD) + ar (ΔBOD)
⇒ ar (ΔABC) = ar (ΔABD)
प्रश्न 5. D, E और F क्रमशः ΔABC की भुजाओं BC, CA और AB के मध्य-बिंदु हैं |
(i) BDEF एक समांतर चतुर्भुज है |
(ii) ar (DEF) = 1/4 ar (ABC)
(iii) ar (BDEF) = 1/2 ar (ABC)
Solution
दिया है: D, E और F क्रमशः ΔABC की भुजाओं BC, CA और AB के मध्य-बिंदु हैं |
सिद्ध करना है:
(i) BDEF एक समांतर चतुर्भुज है |
(ii) ar (DEF) = 1/4 ar (ABC)
(iii) ar (BDEF) = 1/2 ar (ABC)

प्रमाण:
(i) ΔABC में F तथा E भुजाएं AB तथा AC क्रमशः मध्य-बिंदु है|
अतः मध्य-बिंदु प्रमेय से,
FE||BC तथा FE = 1/2 BC
या FE || BC तथा FE = BD [चूँकि D BC का मध्य-बिंदु है]
अत: BDEF एक समांतर चतुर्भुज है |
(यदि किसी चतुर्भुज के सम्मुख भुजाओं के एक युग्म बराबर और समांतर हो तो वह समांतर चतुर्भुज होता है |)
(ii) DF समांतर चतुर्भुज BDEF का विकर्ण है इसलिए,
ar(BDF) = ar(DEF) ...(i)
इसीप्रकार, DCEF भी समान्तर चतुर्भुज है और DE इसका विकर्ण है |
ar(CED) = ar(DEF) ...(ii)
और AEDF भी समान्तर चतुर्भुज है और FE इसका विकर्ण है |
तो ar(AEF) = ar(DEF) ...(iii)
समीकरण (i), (ii) और (iii) से,
ar(AEF) = ar(BDF) = ar(DEF) = ar(CED) ...(iv)
अब, ar(AEF) + ar(BDF) + ar(DEF) + ar(CED) = ar(ABC)
⇒ ar(DEF) + ar(DEF) + ar(DEF) + ar(DEF) = ar(ABC) ...समी० (iv) से
⇒ 4 ar(DEF) = ar(ABC)
⇒ ar(DEF) = 1/4 ar(ABC)
(iii) ar(BDF) + ar(DEF) + ar(AEF) + ar(CED) = ar(ABC)
⇒ ar(BDF) + ar(DEF) + ar(BDF) + ar(DEF) = ar(ABC)
⇒ ar(BDEF) + ar(BDEF) = ar(ABC)
⇒ 2 ar(BDEF) = ar(ABC)
⇒ ar(BDEF) = 1/2 ar(ABC)
प्रश्न 6. आकृति 9.25 में, चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है | यदि AB = CD है, तो दर्शाइए कि:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB या ABCD एक समांतर चतुर्भुज है |
Solution
दिया है: चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है | यदि AB = CD है |
सिद्ध करना है:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB या ABCD एक समांतर चतुर्भुज है |
प्रमाण:
(i) ΔDOC तथा ΔAOB में,
CD = AB (दिया है)
OD = OB (दिया है)
∠COD = ∠AOB (शीर्षाभिमुख कोण)
इसलिए SAS सर्वांगसमता नियम से,
ΔDOC ≅ ΔAOB
∠DCO = ∠BAO ...(i) [CPCT से]
चूँकि ΔDOC ≅ ΔAOB इसलिए,
ar (DOC) = ar (AOB) ...(ii) (सर्वांगसम त्रिभुज क्षेत्रफल में बराबर होते है)
(ii) समी० (ii) दोनों तरफ ar(BOC) जोड़ने पर,
ar (DOC) + ar(BOC) = ar (AOB) + ar(BOC)
⇒ ar(DCB) = ar (ACB)
(iii) समी० (i) से
∠DCO = ∠BAO ...(एकांतर कोण)
इसलिए, CD || AB और CD = AB दिया है |
अत: ABCD एक समांतर चतुर्भुज है |
(सम्मुख भुजाओं के एक युग्म बराबर और समांतर हो तो वह समांतर चतुर्भुज होता है)
इसलिए DA || CB या ABCD एक समांतर चतुर्भुज है |
प्रश्न 7. बिंदु D और E क्रमश: DABC कि भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar(DBC) = ar(EBC) है | दर्शाइए कि DE || BC है |
Solution
दिया है, बिन्दु D और E क्रमश: ΔABC की भुजाओं AB और AC पर इस प्रकार स्थित हैं ar (DBC) = ar (EBC) है।

इस प्रकार, ΔDBC तथा ΔEBC क्षेत्रफल में बराबर तथा समान आधार BC रखते हैं।
अतः
ΔDBC का D से शीर्षलम्ब = ΔEBC का E से शीर्षलम्ब
अतः ΔDBC तथा ΔEBC समान समान्तर रेखाओं के मध्य स्थित है।
अर्थात्, DE || BC
प्रश्न 8. XY त्रिभुज ABC की भुजा BC के समांतर एक रेखा है | यदि BE || AC और CF || AB रेखा XY से क्रमश: E और F पर मिलती है, तो दर्शाइए कि:
ar(ABE) = ar(ACF)
Solution
दिया है, एक ΔABC जिसमें XY || BC तथा BE || AC या BE|| CY तथा CF || AB अर्थात् CF || XB है।
अब चूँकि XY || BC तथा CY || BE है |
इसलिए, EYCB एक समान्तर चतुर्भुज है।
चूँकि, ΔABE तथा समान्तर चतुर्भुज EYCB समान आधार BE तथा समान समान्तर रेखाओं BE तथा AC के मध्य स्थित है।
अतः
ar (ΔABE) = ½ ar (EYCB) ...(i)
पुनः, CF || AB तथा XF || BC
इसलिए BCFX एक समान्तर चतुर्भुज है
चूँकि, ΔACF तथा समान्तर चतुर्भुज BCFX समान आधार CF तथा समान समान्तर रेखाओं AB तथा FC के मध्य स्थित है।
∴ ar (ΔACF) = ½ ar (BCFX) ...(ii)
अब, समान्तर चतुर्भुज BCFX तथा समान्तर चतुर्भुज BCYE समान आधार BC तथा समान समान्तर रेखाओं BC तथा EF के मध्य स्थित है।
∴ ar(BCFX) = ar(BCYE) ...(iii)
समी (i), (ii) तथा (ii) से,
ar (ΔABE) = ar (ΔACF)
प्रश्न 9. समान्तर चतुर्भुज ABCD की एक भुजा AB को एक बिंदु P तक बढाया गया है | A से होकर CP के समांतर खिंची गई रेखा बढाई गई CB को Q पर मिलती है और फिर समांतर चतुर्भुज PBQR (देखिये आकृति 9.26) को पूरा किया गया है | दर्शाइए कि ar(ABCD) = ar(PBQR) है |
[संकेत: AC और PQ को मिलाइए | अब ar(ACQ) और ar(APQ) कि तुलना कीजिये |]
Solution
दिया है, दो समान्तर चतुर्भुज ABCD तथा PBQR हैं।
AC तथा PQ को मिलाते हैं। चूँकि PQ तथा AC क्रमशः समान्तर चतुर्भुज PBQR तथा समान्तर चतुर्भुज ABCD के विकर्ण हैं। अतः
ar (ΔABC) = ½ ar (ABCD) ...(i)
[चूँकि एक समान्तर चतुर्भुज का विकर्ण इसे बराबर क्षेत्रफलों के दो त्रिभुजों में विभाजित करता है |
तथा, ar(ΔPBQ ) = ½ ar (PBQR) ...(ii)
अब, ΔACQ तथा ΔAQP समान आधार AQ तथा समान समान्तर रेखाओं AQ और CP के मध्य स्थित है।
∴ ar (ACQ) = ar (AQP)
⇒ ar (ACQ) – ar (ABQ) = ar (AQP) – ar (ABQ)
[दोनों पक्षों में ar (ΔABQ) को घटाने पर]
⇒ ar (ΔABC) = ar (ΔBPQ)
⇒ ½ ar (ABCD) = ½ ar (PBQR) [समी (i) तथा (ii) से]
⇒ ar (ABCD) = ar (PBQR)
प्रश्न 10. एक समलंब ABCD, जिसमें AB || DC हैं, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं | दर्शाइए कि ar(AOD) = ar(BOC) है |
Solution
दिया है, एक समलम्ब ABCD, जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं।
अब, ΔABC तथा ΔABD समान आधार AB तथा समान समान्तर रेखाओं AB तथा DC के मध्य स्थित हैं।
∴ ar (ΔABD) = ar (ΔABC)
दोनों पक्षों में से ar (ΔAOB) को घटाने पर,
ar(ΔABD) – ar (ΔAOB) = ar (ΔABC) – ar (ΔAOB)
⇒ ar(ΔAOD) = ar(ΔBOC)
प्रश्न 11. आकृति 9.27 में, ABCDE एक पंचभुज है| B से होकर AC के समांतर खिंची गई रेखा बढाई गई DC को F पर मिलती है |

दर्शाइए कि:
(i) ar(ACB) = ar(ACF)
(ii) ar(AEDF) = ar(ABCDE)
Solution
दिया है: ABCDE एक पंचभुज है| B से होकर AC के समांतर खिंची गई रेखा बढाई गई DC को F पर मिलती है |
सिद्ध करना है:
(i) ar(ACB) = ar(ACF)
(ii) ar(AEDF) = ar(ABCDE)
प्रमाण:
AC || BF दिया है |
ΔACB और ΔACF एक ही आधार AC तथा AC || BF के बीच स्थित है |
अत: ar(ACB) = ar(ACF) ...(i)
(एक ही आधार और एक ही समांतर रेखाओं मध्य स्थित त्रिभुज क्षेत्रफल में बराबर होते हैं |)
अब दोनों तरफ ar(ACDE) जोड़ने पर,
ar(ACB) + ar(ACDE) = ar(ACF) + ar(ACDE)
⇒ ar(ABCDE) = ar(AEDF)
⇒ ar(AEDF) = ar(ABCDE)
प्रश्न 12. गाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखंड था। उस गाँव की ग्राम पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केन्द्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबन्ध् के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखंड के संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
Solution
माना ABCD एक चतुर्भुजाकार भूखण्ड है। माना गाँव की ग्राम पंचायत ने उसके भूखण्ड के एक कोने D से उसका कुछ भाग ADE लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केन्द्र का निर्माण कराया जा सके।
अब, AC को मिलाते हैं तथा एक रेखा खींचते हैं जो बिन्दु D से होकर जाती है और BC को आगे बढ़ाने पर बिन्दु P पर मिलती है तथा AC के समान्तर है, तब इतवारी को इस भाग के बदले ECP भूखण्ड के संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखण्ड ABP त्रिभुजाकार हो जाए, तब
ar (ΔADE) = ar (ΔPEC)
अब, ΔDAP तथा ΔDCP समान आधार DP तथा समान समान्तर रेखाओं DP तथा AC के मध्य स्थित है।
∴ ar (ΔDAP) = ar (ΔDCP)
⇒ ar (ΔDAP) – ar (ΔDEP) = ar (ΔDCP) – ar (ΔDEP) (दोनों पक्षों से समान क्षेत्रफल घटाने पर)
⇒ ar (ΔADE) = ar (ΔPCE)
⇒ ar (ΔDAE) + ar (ABCD) = ar (ΔPCE) + ar (ABCE) (दोनों पक्षों में समान क्षेत्रफल जोड़ने पर)
⇒ ar (ABCD) = ar (ΔABP)
प्रश्न 13. ABCD एक समलंब है, जिसमें AB || DC है और AC के समांतर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है | सिद्ध कीजिए कि
ar (ADX) = ar (ACY) है |
[संकेत : CX को मिलाइए]
Solution
दिया है, ABCD एक समलम्ब है, जिसमें AB || DC तथा XY || AC है, अब CX को मिलाते हैं।
चूँकि ΔADX तथा ΔACX समान आधार AX तथा समान समान्तर रेखाओं AB तथा DC के मध्य स्थित हैं।
∴ ar (ΔADX) = ar (ΔACX) ...(i)
पुनः ΔACX तथा ΔACY समान आधार AC तथा समान समान्तर रेखाओं AC तथा XY के मध्य स्थित हैं।
∴ ar (ΔACX) = ar (ΔACY) ...(ii)
समी (i) तथा (ii) से,
ar (ΔADX) = ar (ΔACY)
प्रश्न 14. आकृति 9.28 में, AP || BQ || CR है | सिद्ध कीजिए कि:
ar(AQC) = ar(PBR) है |
Solution
दी गई आकृति के अनुसार,
ar (ΔPBR) = ar (ΔPBQ) + ar (ΔQBR) ...(i)
तथा, ar (ΔAQC) = ar (ΔAQB) + ar (ΔBQC) ...(ii)
चूँकि, ar (ΔBQC) = ar (ΔQBR) ...(iii)
(चूँकि ΔBQC तथा ΔQBR समान आधार BQ तथा समान समान्तर रेखाओं BQ तथा CR के मध्य स्थित हैं।)
इसी प्रकार,
ar (ΔAQB) = ar (ΔPBQ) ...(iv)
समी (iii) तथा (iv) को जोड़ने पर,
ar (ΔBQC) + ar (ΔAQB) = ar (ΔQBR) + ar (ΔPBQ)
समी (i) तथा (ii) से मानों को रखने पर,
ar (ΔAQC) = ar (ΔPBR)
प्रश्न 15. चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि ar (AOD) = ar (BOC) है | सिद्ध कीजिए कि ABCD एक समलंब है |
Solution
दिया है, चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर प्रतिच्छेद करते हैं। तब,
ar (ΔAOD) = ar (ΔBOC)
दोनों पक्षों में ar (ΔAOB) जोड़ने पर,
ar (ΔAOD) + ar (ΔAOB) = ar (ΔBOC) + ar (ΔAOB)
ar (ΔADB) = ar (ΔACB)
अब, ΔACB तथा ΔADB समान आधार AB पर स्थित है।
तथा, ar (ΔADB) = ar (ΔACB)
अतः ΔACB तथा ΔADB समान समान्तर रेखाओं के मध्य स्थित हैं
∴ AB || DC
अत: ABCD एक समलम्ब है।
प्रश्न 16. आकृति 9.29 में, ar(DRC) = ar(DPC) है और ar(BDP) = ar(ARC) है | दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलंब है |

Solution
दिया है,
ar (ΔDPC) = ar (ΔDRC) ...(i)
तथा, ar (ΔBDP) = ar (ΔARC) ...(ii)
समी (ii) में से समी (i) को घटाने पर,
ar (ΔBDP) – ar (ΔDPC) = ar (ΔARC) – ar (ΔDRC)
⇒ ar (ΔBDC) = ar (ΔADC)
चूँकि ये दोनों त्रिभुज समान आधार DC पर स्थित हैं।
∴ DC || AB
अत: ABCD एक समलम्ब है।
∴ ar (ΔDRC) = ar (ΔDPC)
चूँकि दोनों त्रिभुज समान आधार DC रखते हैं।
∴ RP || DC
अत: PRCD एक समलम्ब है।