RD Sharma Solutions Chapter 12 Heights and Distances Exercise 12.1 Class 10 Maths

Chapter Name | RD Sharma Chapter 12 Heights and Distances |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 12.1 Solutions
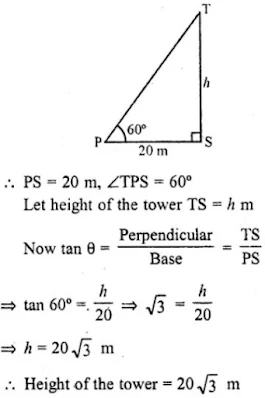
1. A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 60°. What is the height of the tower ?
Solution
Distance between point of observation and foot of tower = 20m = PS
Angle of elevation of top of tower = 60° = 0
Height of tower (h) = ? = TS
2. The angle of elevation of a ladder leaning against a wall is 60° and the foot of the ladder is 9.5 m away from the wall. Find the length of the ladder.
Solution
Let LN is the wall.
Length of the tower (x) = ? = LM
Angle of elevation of ladder = 60°
3. A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2 m away from the wail and the ladder is making an angle of 60° with the level of the ground. Determine the height of the wall.
Solution
Let LN be the height of the wall = h mAngle of elevation of ladder = 60°
Distance of ladder from the foot of the wall = MN = 2m

4. An electric pole is 10 m high. A steel wire tied to top of the pole is affixed at a point on the ground to keep the pole up right. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
Solution
Height of the electric pole AB = 10m
Length of the steel wire AC = x m
Angle made by wire with the foot of the pole = 45°
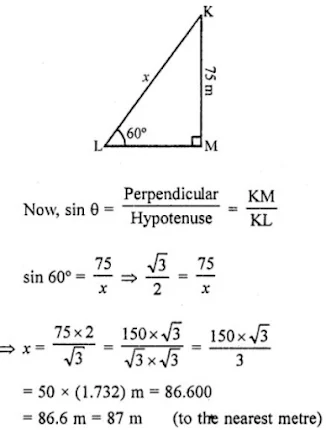
5. A kite is flying at a height of 75 metres from the ground level, attached to a string inclined at 60° to the horizontal. Find the length of the string to the nearest metre.
Solution
Let K be the kite flying in the sky at a height of 75 m from the ground LM.
Angle made by string KL with the ground = 60°
Length of string KL = x m
Height of the kite from the ground KM = 75 m
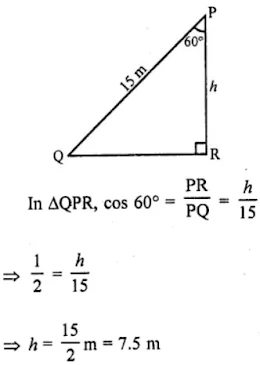
6. A ladder 15 m long just reaches the top of a vertical wall. If the ladders makes an angle of 60° with the wall, then find the height of the wall.
Solution
Height of the ladder = 15 m
Height of the vertical wall = h
Angle of elevation made by the ladder with the wall θ = 60°.
Hence, the required height of the wall is 7.5 m
7. A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff. At a point on the plane 70 metres away from the tower, an observer notices that the angles of elevation of the top and the bottom of the flag-staff are respectively 60° and 45°. Find the height of the flag-staff and that of the tower.
Solution
TR be the tower and FT is the flag on it. P is an point on the ground 70 m away from the foot of the tower.
From P, the angle of elevation of the top and bottom of the flag are 60° and 45° respectively.
Let h be the height of flag staff and x be the height of the tower.
Height of flag staff = 51.24 m
and height of tower = 70 m
8. A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break ?
Solution
Height of the tree TR = 15 m
Let the tree is broken from A and its top T touches the ground at B making an angle of 60° with the ground.
∴ Height of broken tree from the ground = 15.0 - 8.1 = 6.9 m
9. A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height 5 metres. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are respectively 30° and 60°. Find the height of the tower.
Solution
Let TR be the tower and FT is a flag staff on it.
A is a point on the ground such that it makes angles of elevation of the bottom and top of the flag staff of 30° and 60° respectively.
10. A person observed the angle of elevation of the top of a tower as 30°. He walked 50 m towards the root of the tower along level ground and found the angle of elevation of the top of the tower as 60°. Find the height of the tower.
Solution
Height of the tower TR = h
Angle of elevation of the top T of the tower = 30°
At a distance of 50 m at B, the angle of elevation = 60°.
Let h be the height of the tower and BR = x, then AR = (50 + x).
11. The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m longer than when it was 60°. Find the height of the tower.
Solution
Height of the tower TR = h
Shadow of the tower at the elevation of the sun 45° = x m
Shadow of the tower at the elevation of the sun 60° = (x – 10) m.
Now in right ΔTAR,
12. A parachutist is descending vertically and makes angles of elevation of 45° and 60° at two observing points 100 m apart from each other on the left side of himself. Find the maximum height from which he falls and the distance of the point where he falls on the ground from the just observation point.
Solution
P is the position of the parachutist who is landing at Q vertically on the ground.
A and B are two observations point such that AB = 100 m
Angle of elevation from point A = 45°
Angle of elevation from point B = 60°
Let h be the height of the parachutist from the ground and x be the distance of B from Q and (100 + x) is the distance from A to Q.
Now in right ΔAPQ,
13. On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
Solution
Height of the tower TR = 150m
Angle of depression at point A = 45°
Angle of depression at point B = 60°
Distance between A and B = x m
14. The angle of elevation of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 metres towards the foot of the tower, the angle of elevation of the tower becomes 60°. Show that the height of the tower is 129.9 metres (Use √3 = 1.732).
Solution
Height of the tower TR = h
Angle of elevation from point A = 30°
Angle of elevation from point B = 60°
Distance between A and B = 150 m
Let the distance of point B from the foot of the tower be x.
15. The angle of elevation of the top of a tower as observed from a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626]
Solution
Let PQ be the tower and from a points A, and B the angles of elevations of top P of the tower are 32° and 63° respectively and AB= 100 m
Height of tower = 91.66 m
Distance of A from the foot of the tower = 146.7 m