RD Sharma Solutions for Class 10 Maths Chapter 10 Circles MCQs and VSAQs

VSAQs
Answer each of the following questions either in one word or one sentence or as per requirement of the questions :
1. In the figure, PA and PB are tangents to the circle drawn from an external point P. CD is a third tangent touching the circle at Q. If PB = 10 cm and CQ = 2 cm, what is the length PC ?
Solution
In the figure, PA and PB are the tangents to the circle drawn from P
CD is the third tangent to the circle drawn at Q
PB = 10 cm, CQ = 2 cm
PA and PB are tangents to the circle
PA = PB = 10 cm
Similarly CQ and CA are tangents to the circle
CQ = CA = 2 cm
PC = PA – CA = 10 – 2 = 8 cm
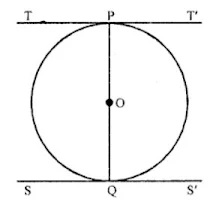
2. What is the distance between two parallel tangents of a circle of radius 4 cm ?
Solution
TT’ and SS’ are two tangents of a circle with centre O and radius 4 cm and TT’ || SS’
OP and OQ are joined
Now OP is the radius and TPT’ is the tangent
OP ⊥ TPT’
Similar OQ ⊥ SS’
But TT’ || SS’
POQ is the diameter
Which is 4×2 = 8 cm
Distance between the two parallel tangents is 8 cm
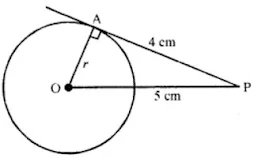
3. The length of tangent from a point A at a distance of 5 cm from the centre of the circle is 4 cm. What is the radius of the circle ?
Solution
PA is a tangent to the circle from P at a distance of 5 cm from the centre O
PA = 4 cm
OA is joined and let OA = r
Now in right ∆OAP,
OP² = OA² + PA²
⇒ (5)² = r² + (4)²
⇒ 25 = r + 16
⇒ r² = 25 – 16 = 9 = (3)²
r = 3
Radius of the circle = 3 cm
4. Two tangents TP and TQ are drawn from an external point T to a circle with centre O as shown in the following figure. If they are inclined to each other at an angle of 100°, then what is the value of ∠POQ ?
Solution
TP and TQ are the tangents from T to the circle with centre O and ∠PTQ = 100°
OT, OP and OQ are joined
OP and OQ are radius
OP ⊥ PT and OQ ⊥ QT
Now in quadrilateral OPTQ,
∠POQ + ∠OPT + ∠PTQ + ∠OQT = 360° (Sum of angles of a quadrilateral)
⇒ ∠POQ + 90° + 100° + 90° = 360°
⇒ ∠POQ + 280° = 360°
⇒ ∠POQ = 360° – 280° = 80°
Hence ∠POQ = 80°
5. What is the distance between two parallel tangents to a circle of radius 5 cm?
Solution
In a circle, the radius is 5 cm and centre is O
TT’ and SS’ are two tangents at P and Q to the circle
Such that TT’ || SS’
Join OP and OQ
OP is radius and TPT’ is the tangent
OP ⊥ TT’
Similarly OQ ⊥ SS’
POQ is the diameter of the circle
Now length of PQ = OP + OQ = 5 + 5 = 10 cm
Hence, distance between the two parallel tangents = 10 cm
6. In Q. No. 1, if PB = 10 cm, what is the perimeter of ∆PCD ?
Solution
In the figure, PB = 10 cm, CQ = 2 cm
PA and PB are tangents to the give from P
PA = PB = 10 cm
Similarly, CA and CQ are the tangents
CA = CQ = 2 cm
and DB and DQ are the tangents
DB = DQ
Now, perimeter of ∆PCD
PC + PD + CQ + DQ
= PC + CQ + PD + DQ
= PC + CA + PD + DB {CQ = CA and DQ = DB}
= PA + PB = 10 + 10 = 20 cm