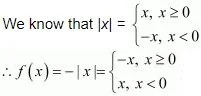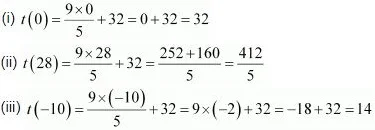NCERT Solutions for Chapter 2 Relations and Functions Class 11 Maths Exercise 2.3

Class 11 Maths NCERT Solutions for Chapter 2 Relations and Functions Exercise 2.3

Relations and Functions Exercise 2.3 Solutions 

1. Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
(i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
(iii) {(1, 3), (1, 5), (2, 5)}

Solution

(i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
Since 2, 5, 8, 11, 14, and 17 are the elements of the domain of the given relation having their unique images, this relation is a function.
Here, domain = {2, 5, 8, 11, 14, 17} and range = {1}

(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
Since 2, 4, 6, 8, 10, 12, and 14 are the elements of the domain of the given relation having their unique images, this relation is a function.
Here, domain = {2, 4, 6, 8, 10, 12, 14} and range = {1, 2, 3, 4, 5, 6, 7}

(iii) {(1, 3), (1, 5), (2, 5)}
Since the same first element i.e., 1 corresponds to two different images i.e., 3 and 5, this relation is not a function.

2. Find the domain and range of the following real function:
(i) f(x) = –|x|
(ii) f(x) = √(9 – x²)

Solution

(i) f(x) = - |x| , x ∈ R 

Since f(x) is defined for x ∈ R, the domain of f is R.
It can be observed that the range of f(x) = –|x| is all real numbers except positive real numbers.
∴The range of f is (–∞, 0].

(ii) f(x) = √(9 – x²)
Since √(9 – x²) is defined for all real numbers that are greater than or equal to -3 and less than or equal to 3, the domain of f(x) is { x : -3 ≤ x ≤ 3} or [-3, 3].
For any value of x such that –3 ≤ x ≤ 3, the value of f(x) will lie between 0 and 3.
∴The range of f(x) is {x: 0 ≤ x ≤ 3} or [0, 3].

3. A function f is defined by f(x) = 2x – 5. Write down the values of
(i) f(0),
(ii) f(7),
(iii) f(–3)

Solution

The given function is f(x) = 2x – 5.
Therefore,
(i) f(0) = 2 × 0 – 5 = 0 – 5 = –5

(ii) f(7) = 2 × 7 – 5 = 14 – 5 = 9

(iii) f(–3) = 2 × (–3) – 5 = – 6 – 5 = –11

4. The function ‘t’ which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by t(C)=9C/5 + 32
Find
(i) t(0)
(ii) t(28)
(iii) t(–10)
(iv) The value of C, when t(C) = 212. 

Solution

The given function is t(C) = 9C/5 + 32 . 
Therefore, 

(iv) It is given that t(C) = 212 

Thus, the value of t, when t(C) = 212, is 100. 

5. Find the range of each of the following functions.
(i) f(x) = 2 – 3x, x ∈ R, x > 0.
(ii) f(x) = x² + 2, x, is a real number.
(iii) f(x) = x, x is a real number

Solution

(i) f(x) = 2 – 3x, x ∈ R, x > 0
The values of f(x) for various values of real numbers x > 0 can be written in the tabular form as

x	0.01	0.1	0.9	1	2	2.5	4	5	…
f(x)	1.97	1.7	–0.7	–1	–4	–5.5	–10	–13	…

Thus, it can be clearly observed that the range of f is the set of all real numbers less than 2.
i.e., range of f = (–∞, 2)
Alter:
Let x > 0
⇒ 3x > 0
⇒ 2 –3x < 2
⇒ f(x) < 2
∴Range of f = (–∞, 2)

(ii) f(x) = x² + 2, x, is a real number
The values of f(x) for various values of real numbers x can be written in the tabular form as

x	0	±0.3	±0.8	±1	±2	±3	…
f(x)	2	2.09	2.64	3	6	11	...

Thus, it can be clearly observed that the range of f is the set of all real numbers greater than 2.
i.e., range of f = [2, ∞)
Alter:
Let x be any real number.
Accordingly,
x² ≥ 0
⇒ x² + 2 ≥ 0 + 2
⇒ x² + 2 ≥ 2
⇒ f(x) ≥ 2
∴ Range of f = [2,)

(iii) f(x) = x, x is a real number
It is clear that the range of f is the set of all real numbers.
∴ Range of f = R