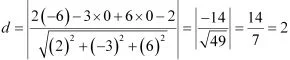Class 12 Maths NCERT Solutions for Chapter 11 Three Dimensional Geometry Exercise 11.3

Three Dimensional Geometry Exercise 11.3 Solutions
1. In following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
(a) z = 2
(b) x + y + z = 1
(c) 2x + 3y - z = 5
(d) 5y + 8 = 0
Solution
(a) The equation of the plane is z = 2 or 0x + 0y + z = 2 ...(1)
The direction ratios of normal are 0, 0, and 1.
∴ √(02 + 02 + 12 = 1)
Dividing both sides of equation (1) by 1, we obtain
0.x + 0.y + 1.z = 2
This is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of the perpendicular drawn from the origin.
Therefore, the direction cosines are 0, 0, and 1 and the distance of the plane from the origin in 2 units.
(b) x + y + z = 1 …(1)
The direction ratios of normal are 1, 1, and 1.
∴ √[(1)2 + (1)2 + (1)2] = √3
Dividing both sides of equation (1) by √3, we obtain
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
Therefore, the direction cosines of the normal are 1/√3, 1/√3, and 1/√3 and the distance of normal from the origin in 1/√3 units.
(c) 2x + 3y - z = 5 ...(1)
The direction ratios of normal are 2, 3, and -1.
√[(2)2 + (3)2 + (-1)2] = √14
Dividing both sides of equation (1) by √14, we obtain
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
Therefore, the direction cosines of the normal to the plane are 2/√14 , 3/√14, and -1/√14 and the distance of normal from the origin is 5/√14 units.
(d) 5y + 8 = 0
⇒ 0x − 5y + 0z = 8 ...(1)
The direction ratios of normal are 0, −5, and 0.
∴ √[0 + (-5)2 + 0 ] = 5
Dividing both sides of equation (1) by 5, we obtain
-y = 8/5
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
Therefore, the direction cosines of the normal to the plane are 0, -1 and 0 and the distance of normal from the origin is 8/5 units.
2. Find the vector equation of a plane which is at a distance of 7 units from the origin and normal to the vector 3i ^+ 5j ^- 6k ^ .
Solution
The normal vector is, r⃗ = 3i ^ + 5j ^ - 6k ^

It is known that the equation of the plane with position vector r⃗ is given by, r⃗ . n ^ = d

This is the vector equation of the required plane.
(a) r⃗ . (i ^ + j ^ - k ^) = 2
(b) r⃗ = (2i ^ + 3j ^- 4k ^) = 1
(c) r⃗ = [(s- 3t)i ^ + (3 - t)j ^ + (2s + t) k ^) = 15

(a) 2x + 3y + 4z - 12 = 0
(b) 3y + 4z - 6 = 0
(c) x + y + z = 1
(d) 5y + 8 = 0
2x + 3y + 4z - 12 = 0
⇒ 2x + 3y + 4z = 12 ...(1)
The direction ratios of normal are 2, 3, and 4.

Dividing both sides of equation (1) by √29, we obtain.
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin,
The coordinates of the foot of the perpendicular are given by (ld, md, nd).
Therefore, the coordinates of the foot of the perpendicular are
3y + 4z - 6 = 0
⇒ 0x + 3y + 4z = 6 ...(1)
The direction ratios of the normal are 0, 3 , and 4 .
Dividing both sides of equation (1) by 5, we obtain
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
The coordinates of the foot of the perpendicular are given by (ld, md, nd).
Therefore, the coordinates of the foot of the perpendicular are
(c) Let the coordinates of the foot of perpendicular P from the origin to the plane be (x1 , y1 , z1 ) .
x + y + z = 1 ...(1)
The direction ratios of the normal are 1, 1, and 1.
Dividing both sides of equation (1) by √3, we obtain
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
The coordinates of the foot of the perpendicular are given by (ld, md, nd).
Therefore, the coordinates of the foot of the perpendicular are
(d) Let the coordinates of the foot of perpendicular P from the origin to the plane be (x1 , y1 , z1 ) .
5y + 8 = 0
⇒ 0x - 5y + 0z = 8 ...(1)
The direction ratios of the normal are 0, -5, and 0.
Dividing both sides of equation (1) by 5, we obtain
-y = 8/5
This equation is of the form lx + my + nz = d , where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
Therefore, the coordinates of the foot of the perpendicular are
(a) that passes through the point (1, 0, −2) and the normal to the plane is i ^+ j ^- k ^
(b) that passes through the point (1, 4, 6) and the normal vector to the plane is i ^- 2j ^+ k ^
The normal vector N⃗ perpendicular to the plane is N⃗ = i ^ + j ^ - k ^
The vector equation of the plane is given by, ( r⃗ - a⃗).N⃗ = 0
r⃗ is the position vector of any point P (x, y, z) in the plane.
∴ r⃗ = xi ^ + yj ^ + zk ^
Therefore, equation (1) becomes

⇒ (x - 1) + y - (z + 2) = 0
⇒ x + y - z - 3 = 0
⇒ x + y - z = 3
This is the Cartesian equation of the required plane.
The vector equation of the plane is given by, (r⃗ - a⃗).N⃗ = 0.
∴ r⃗ = xi ^ + yj ^ + zk ^
Therefore, equation (1) becomes

⇒ (x - 1) - 2 (y - 4) + (z - 6) = 0
⇒ x - 2y + z + 1 = 0
This is the Cartesian equation of the required plane.
(a) (1, 1, −1), (6, 4, −5), (−4, −2, 3)
(b) (1,1,0), (1 , 2 , 1 ), (-2, 2, -1 )

= 2 + 2 - 4
= 0
Since, A, B, C are collinear points, there will be infinite number of planes passing through the given points.

Therefore, a plane will pass through the points A, B, and C.

⇒ (-2) (x - 1) - 3 (y - 1) + 3z = 0
⇒ -2x - 3y + 3z + 2 + 3 = 0
⇒ -2x - 3y + 3z = - 5
⇒ 2x + 3y - 3z = 5
This is the Cartesian equation of the required plane.
Dividing both sides of equation (1) by 5, we obtain

It is known that the equation of a plane in intercept form is x/a + y/b + z/c = 1, where a, b, c are the intercepts cut off by the plane at x, y, and z axes respectively.
Therefore, for the given equation,
a = 5/2, b = 5, and c = -5
Thus, the intercepts cut off by the plane are 5/2, 5 and -5.
The equation of the plane ZOX is y = 0
Any plane parallel to it is of the form, y = a
Since the y-intercept of the plane is 3,
∴ a = 3
Thus, the equation of the required plane is y = 3
9. Find the equation of the plane through the intersection of the planes 3x – y + 2z – 4 = 0 and x + y + z – 2 = 0 and the point (2, 2, 1).
Solution
The equation of any plane through the intersection of the planes,
3x - y + 2z - 4 = 0 and x + y + z - 2 = 0, is
(3x - y + 2z - 4 ) + α (x + y + z - 2) = 0, where α ∈ R ...(1)
The plane passes through the point (2, 2, 1). Therefore, this point will satisfy equation (1).
∴ (3×2 - 2 + 2×1 - 4) + α (2 + 2 + 1 - 2) = 0
⇒ 2 + 3α = 0
⇒ α = -2/3
Substituting α = -2/3 in equation (1), we obtain
(3x - y + 2z - 4) - 2/3 (x + y+ z - 2) = 0
⇒ 3(3x - y + 2z - 4) - 2(x + y + z - 2) = 0
⇒ (9x - 3y + 6z - 12) - 2(x + y + z - 2) = 0
⇒ 7x - 5y + 4z - 8 = 0
This is the required equation of the plane.
10. Find the vector equation of the plane passing through the intersection of the planes
r⃗.(2i ^+2j ^- 3k ^) = 7, r⃗. (2i ^+ 5j ^+ 3k ^) = 9 and through the point (2, 1, 3)
Solution
The equations of the planes are r⃗ .(2i ^ + 2j ^ - 3k ^) = 7 and r⃗ .(2i ^ + 5j ^ + 3k ^) = 9
The equation of any plane through the intersection of the planes given in equations (1) and (2) is given by,
The plane passes through the point (2, 1, 3). Therefore, its position vector is given by ,
r⃗ = 2i ^ + 2j ^ - 3k ^
Substituting, in equation (3), we obtain
⇒ (2 + 2λ) + (2 + 5λ) + (3λ - 3) = 9λ + 7
⇒ 18λ - 3 = 9λ + 7
⇒ 9λ = 10
⇒ λ = 10/9
Substituting λ = 10/9 in equation (3), we obtain
This is the vector equation of the required plane.
11. Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x − y + z = 0. Also find the distance of the plane, obtained above, from the origin.
Solution
The equation of the plane through the intersection of the planes, x + y + z = 1 and 2x + 3y + 4z = 5 is
(x + y + z -1) + λ(2x + 3y + 4z- 5) = 0
⇒ (2λ + 1 )x + (3λ + 1)y + (4λ + 1)z - (5λ + 1) = 0 ...(1)
The direction ratios, a1, b1, c1, of this plane are (2λ + 1), (3λ + 1), and (4λ + 1).
The plane in equation (1) is perpendicular to x - y + z = 0
Its direction ratios, a2, b2, c2, are 1, −1, and 1.
Since the planes are perpendicular,
a1a2 + b1b2 + c1c2 = 0
⇒ (2λ + 1) - (3λ + 1) + (4λ + 1) = 0
⇒ 3λ + 1 = 0
⇒ λ = -1/3
Substituting λ = -1/3 in equation (1), we obtain
⇒ x - z + 2 = 0
This is the required equation of the plane.
12. Find the angle between the planes whose vector equations are r⃗ .(2i ^+ 2j ^- 3k ^) = 5 and r ^.(3i ^- 3j ^+ 5k ^) = 3
Solution
The equations of the given planes are r⃗ .(2i ^ + 2j ^ - 3k ^) = 5 and r ^.(3i ^- 3j ^+ 5k ^) = 3
It is known that if n1⃗ and n2⃗ are normal to the planes r⃗ .n1⃗ = d1, and r⃗ .n2⃗ = d2, then the angle between them, Q, is given by,
Substituting the value of n⃗ .n2⃗ , |n1⃗| and |n2⃗| in equation (1), we obtain
13. Find the angle between the planes whose vector equation are r⃗ . (2i ^ + 2j ^ - 3k ^) = 5 and r ^.(3i ^ - 3j ^+ 5k ^) = 3
(a) 7x + 5y + 6z + 30 = 0 and 3x - y - 10z + 4 = 0
(b) 2x + y + 3z - 2 = 0 and x - 2y + 5 = 0
(c) 2x - 2y + 4z + 5 = 0 and 3x - 3y + 6z - 1 = 0
(d) 2x - y + 3z - 1 = 0 and 2x - y + 3z + 3 = 0
(e) 4x + 8y + z - 8 = 0 and y + z - 4 = 0
Solution
The direction ratios or normal to the plane, L1 : a1x + b1y + c1z = 0 , are a1, b1, c1 and L2: a1x + b2y + c2z = 0 are a2, b2, c2.
(a) The equations of the planes are 7x + 5y + 6z + 30 = 0 and 3x - y - 10z + 4 = 0
Here, a1 = 7, b1 = 5 , c1 = 6 and a2 = 3, b2 = -1 , c2 = -10
a1a2 + b1b2 + c1c2 = 7×3 + 5×(-1) + 6×(-10) = -44 ≠ 0
Therefore, the given planes are not perpendicular.
Therefore, the given planes are not parallel.
The angle between them is given by,
(b) The equations of the planes are 2x+ y + 3z - 2 = 0 and x - 2y + 5 = 0
Here, a1 = 2, b1 = 1, c1 = 3 and a2 = 1, b2 = -2, c2 = 0
∴ a1a2 + b1b2 + c1c2 = 2×1 + 1× (-2) + 3×0 = 0
Thus, the given planes are perpendicular to each other.
(c) The equations of the given planes are 2x - 2y + 4z + 5 = 0 and 3x - 3y + 6z - 1 = 0
a1 = 2, b1 = -2, c1 = 4 and a2 = 3, b2 = -3, c2 = 6
a1a2 + b1b2 + c1c2 = 2×3 + (-2) (-3) + 4×6 = 6 + 6 + 24 = 36 ≠ 0
Thus, the given planes are not perpendicular tot each other.
Thus, the given planes are parallel to each other.
(d) The equations of the planes are 2x - y + 3z - 1 = 0 and 2x - y + 3z + 3 = 0
Here, a1 = 2, b1 = -1, c1 = 3 and a2 = 2, b2 = -1, c2 = 3
Thus, the given lines are parallel to each other.
(e) The equations of the given planes are 4x + 8y + z - 8= 0 and y + z - 4= 0
Here, a1 = 4, b1 = 8 , c1 = 1 and a2 = 0, b2 = 1 , c2 = 1
a1a2 + b1b2 + c1c2 = 4×0 + 8×1 + 1 = 9 ≠ 0
Therefore, the given lines are not perpendicular to each other.
Therefore, the given lines are not parallel to each other.
The angle between the planes is given by,
14. In the given cases, find the distance of each of the given points from the corresponding given plane.
Point Plane
(a) (0, 0, 0) 3x – 4y + 12z = 3
(b) (3, – 2, 1) 2x – y + 2z + 3 = 0
(c) (2, 3, – 5) x + 2y – 2z = 9
(d) (– 6, 0, 0) 2x – 3y + 6z – 2 = 0
Solution
It is known that the distance between a point, p(x1, y1, z1) and a plane, Ax + By + Cz = D, is given by,
(a) The given point is (0, 0, 0) and the plane is 3x - 4y + 12z = 3
(b) The given points is (3, -2, 1) and the plane is 2x - y + 2z + 3 = 0
Therefore,
(c) The given point is (2, 3, -5) and the plane is x + 2y - 2z = 9
(d) The given point is (-6, 0, 0)and the plane is 2x - 3y + 6z - 2 = 0