Chapter 9 Some Applications of Trigonometry Important Questions for CBSE Class 10 Maths Board Exams
This page contains Important Questions for Class 10 Maths Chapter 9 Some Applications of Trigonometry, which will help the students to prepare for the CBSE Class 10 maths Board exam 2022-23. It help the doing better in their maths paper. Extra questions of Chapter 9 Some Applications of Trigonometry given here which are based on the pattern of CBSE NCERT book. Students will learn about the entire syllabus and learn how to solve problems in preparation for the exams.

Important Questions for Chapter 9 Some Applications of Trigonometry Class 10 Maths
Important Questions Class 10 Maths contains all types of questions which could be asked in the examination. We have included short answer questions as well as long answer questions for Chapter 9 Some Applications of Trigonometry. For more exercise, students can also refer to the Coordinate Geometry NCERT Solutions. Students can solve these questions and check their answers on the website. All the questions are solved in detail.
Some Applications of Trigonometry Class 10 Maths Important Questions Very Short Answer (1 Mark)
1. A ladder 15 m long leans against a wall making an angle of 60º with the wall. Find the height of the point where the ladder touches the wall.Solution
Let the height of wall be h. As per given in question we have drawn figure below.

2. A ladder, leaning against a wall, makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.
Solution
Let AC be the ladder
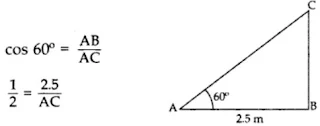
∴ Length of ladder, AC = 5 m
3. If the length of the ladder placed against a wall is twice the distance between the foot of the ladder and the wall. Find the angle made by the ladder with the horizontal.
Solution
Let the distance between the foot of the ladder and the wall is x, then length of the ladder will be 2x. As per given in question we have drawn figure be

4. A ladder, leaning against a wall, makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.
Solution
As per given in question we have drawn figure below.

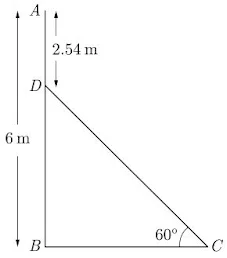
5. In the given figure, AB is a 6 m high pole and DC is a ladder inclined at an angle of 60° to the horizontal and reaches up to point D of pole. If AD = 2.54 m, find the length of ladder. (use √3 = 1.73)
Solution
We have,
AD = 2.54 m
DB = 6 - 2.54 = 3.46 m
In △BCD,
∠B = 90°

Thus length of ladder is 4 m.
6. An observer 1.5 m tall is 28.5 m away from a tower 30 m high. Find the angle of elevation of the top of the tower from his eye.

Solution
As per given in question we have drawn figure below.
Here,
AE = 1.5 m is height of observer and BD = 30 m is tower.
Now,
BC = 30 - 1.5 = 28.5 m
In △BAC,
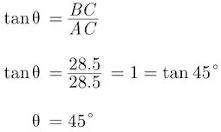
Hence, angle of elevation is 45°.
7. If a tower 30 m high, casts a shadow 10√3 m long on the ground, then what is the angle of elevation of the sun?
Solution
Let required angle be θ.

⇒ tan θ = tan 60°
∴ θ = 60°
8. The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x : y.
Solution
When base is same for both towers and their heights are given, i.e., x and y respectively
Let the base of towers be k.

9. A pole 6 m high casts a shadow 2√3 m long on the ground, then find the Sun’s elevation.
Solution
Let the Sun’s elevation be θ. As per given in question we have drawn figure below.

Length of pole is 6 m and length of shadow is 2√3 m.
From △ABC we have,

Hence sun’s elevation is 60°.
