Chapter 6 Triangles Important Questions for CBSE Class 10 Maths Board Exams
This page contains Important Questions for Class 10 Maths Chapter 6 Triangles, which will help the students to prepare for the CBSE Class 10 maths Board exam 2022-23. It help the doing better in their maths paper. Extra questions of Chapter 6 Triangles given here which are based on the pattern of CBSE NCERT book. Students will learn about the entire syllabus and learn how to solve problems in preparation for the exams.
Important Questions for Chapter 6 Triangles Class 10 Maths
Important Questions Class 10 Maths contains all types of questions which could be asked in the examination. We have included short answer questions as well as long answer questions for Chapter 6 Triangles. For more exercise, students can also refer to the Triangles NCERT Solutions. Students can solve these questions and check their answers on the website. All the questions are solved in detail.
Triangles Class 10 Maths Important Questions Very Short Answer (1 Mark)
1. In Figure, DE||BC. Find the length of side AD, given that AE = 1.8 cm, BD = 72 cm and CE = 5.4 cm.


Solution
Since,DE||BC, we have
AD/DB = AE/EC
Substituting the values, we get

2. △ABC is isosceles with AC = BC. If AB2 = 2 AC2, then find the measure of ∠C.
Solution
We have,
AB2 = 2 AC2
⇒ AB2 = AC2 + AC2
⇒ AB2 = BC2 + AC2 (BC = AC)
It satisfies the Pythagoras theorem. Thus according to converse of Pythagoras theorem, △ABC is a right angle triangle and ∠C = 90°.
3. In the given figure, if ∠A = 90°, ∠B = 90°, OB = 4.5 cm, OA = 6 cm and AP = 4 cm then find QB.


Solution
In PAO and QBO, we have
∠A = ∠B = 90°
Vertically opposite angle,
∠POA = ∠QOB
Thus, QB = 3 cm

Thus, △PAO ~ △QBO
4. If ∆ABC ~ ∆PQR, perimeter of ∆ABC = 32 cm, perimeter of ∆PQR = 48 cm and PR = 6 cm, then find the length of AC.
Solution
∆ABC ~ ∆PQR (Given)

⇒ AC = 4 cm
5. In ∆ABC DE|| BC, find the value of x.
Solution
In the given figure DE|| BC, thus

⇒ x = 3
6. In the given figure, if ∠A = 90°, B = 90, OB = 4.5 cm, OA = 6 cm and AP = 4 cm then find QB.

Solution
In ∆PAO and ∆QBO we have,
∠A = ∠B = 90°
Vertically opposite angle,
∠POA = ∠QOB
Thus,
∆PAO ∼ ∆QBO

Thus QB = 3 cm
7. In ∆ABC if X and Y are points on AB and AC respectively such that AX/XB = 3/4, AY = 5 and YC = 9, then state whether XY and BC parallel or not.
Solution
As per question we have drawn figure given below.

In this figure we have,

8. If triangle ABC is similar to triangle DEF such that 2AB = DE and BC = 8 cm then find EF.
Solution

As per given condition we have drawn the figure below.
Here,
we have 2AB = DE and BC = 8 cm
Since ∆ABC ~ ∆DEF, we have

9. If ∆ABC ~ ∆RPQ, AB = 3 cm, BC = 5 cm, AC = 6 cm, RP = 6 cm and PQ = 10, then find QR.
Solution
∆ABC ~ ∆RPQ …[Given]

∴ QR = 12 cm
10. In ∆ABC, DE || BC, find the value of x.

Solution
In ∆ABC, DE || BC …[Given]
 ⇒ x(x + 5) = (x + 3)(x + 1)
⇒ x(x + 5) = (x + 3)(x + 1)
⇒ x2 + 5x = x2 + 3x + x + 3
⇒ x2 + 5x – x2 – 3x – x = 3
∴ x = 3 cm

⇒ x2 + 5x = x2 + 3x + x + 3
⇒ x2 + 5x – x2 – 3x – x = 3
∴ x = 3 cm
11. If triangle ABC is similar to triangle DEF such that 2AB = DE and BC = 8 cm then find EF.

Solution
As per given condition we have drawn the figure below.
Here we have,
2AB = DE and BC = 8 cm
Since,
∆ABC ~ ∆DEF, we have
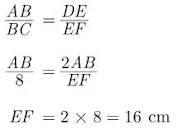
Triangles Class 10 Maths Important Questions Short Answer-I (2 Marks)
12. In an equilateral triangle of side 3√3 cm find the length of the altitude.
Solution
Let ∆ABC be an equilateral triangle of side 3√3 cm and AD is altitude which is also a perpendicular bisector of side BC. This is shown in figure given below.

13. In an equilateral triangle of side 24 cm, find the length of the altitude.
Solution
Let ∆ABC T be an equilateral triangle of side 24 cm and AD is altitude which is also a perpendicular bisector of side BC. This is shown in figure given below.


