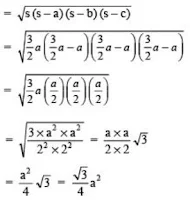Revision Notes of Chapter 12 Heron's Formula Class 9th Math
Topics in the Chapter- Basics Revision
- Area of Triangle
- Heron's Formula
- Area of equilateral Triangle
• Area of a triangle = 1/2 × Base × Height
• Heron’s formula: For sides of a triangle being a, b, c:
Area of Triangle =

where s is semi-perimeter and s = (a+b+c)/2
• For finding area of a quadrilateral we divide it into various triangles. Then we use Heron’s formula to find the area of the triangles.
Area of Triangles

= 1/2 × (side) × [altitude corresponding to that side (or height)]
= 1/2 × BC × AD
= 1/2 × a × h
Thus, area of a triangle = 1/2 × Base × Height
Note:
Unit of measurement for area of any plane figure is taken as square metre (m2) or square centimetre (cm2), etc.
Area of Triangle using Heron's Formula
When it is not possible to find the height of the triangle easily and measures of all the three sides are known then we use Heron’s formula, which is given by:
Area of a triangle =

where a, b and c are the sides of the triangle and s = semi-perimeter, i.e. half the perimeter of the triangle = (a+b+c)/2
Area of an Equilateral Triangle
Let the side of the equilateral triangle be ‘a’.