NCERT Solutions for Class 11 Maths Chapter 3 Trigonometric Functions Exercise 3.1
Chapter 3 Trigonometric Functions Exercise 3.1 Class 11 Maths NCERT Solutions is available here that will serve every student in completing their homework on time. NCERT Solutions for Class 11 Maths is an essential resources for the preparation for higher classes and competitive examinations. A student must practice all these in order to stand out in Maths subject.
1. Find the radian measures corresponding to the following degree measure.
(i) 25°
(ii) –47°30'
(iii) 240°
(iv) 520°
Answer
Ï€ radians = 180°
1° = Ï€/180 radians
(i) 25° = 25 × Ï€/180 = 5Ï€/36
(ii) 60' = 1° ∴ 30' = 30°/60 = 1/2
∴ 47° 30' = (47 + 1/2)° = (95/2)°
∴ 180° = Ï€ radian
-(95/2) = -Ï€/ 180 × 95/2 radians = -19Ï€/72 radians
(iii) 240° = 240 × Ï€/180 = 4Ï€/3 radians.
(iv) 180° = Ï€ radians
520° = Ï€/180 × 520 radians = 26Ï€/9 radians
2. Find the degree measures corresponding to the following radian measures (use π = 22/7).
(i) 11/16
(ii) – 4
(iii) 5Ï€/ 3
(iv) 7Ï€/6
Answer
(i) Ï€ radians = 22/7 radians = 180°
∴ 11/16 radians = 180/ 22 × 7× 11/16 degree
=315/8 degree = 39.3/8 degree
= 39°22°30°
(ii) -4 radians = (-4 × 180/Ï€)°
= (4 × 180 × 7)/ 22 = -(2520/11) = 229° 5' 27'' (nearly)
(iii) Similar
(iv) Similar
3. A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
Answer
Angle rotated in one revolution = 2Ï€ radians
∴ Angle rotated in 360 revolution
= 360 × 2Ï€ radians
⇒ Angle turned in one minute or 60 sec
= 360 × 2Ï€
Hence, angle turned in 1sec= (360 × 2Ï€)/60
= 12Ï€ radians.
4. Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm (use π = 22/7).
Answer
We know that l = r θ
where l = length of arc = 20 cm;
r = radius of circle = 100 cm;
θ = angle subtended at the centre
∴ θ = l/r = 22/100 = 0.22 radians
= 0.22 × 180°/ degree
= (0.22 × 180 × 7)/22 = 22/100 × (180 × 7)/22
126/10 = 12°36’
5. In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.
Answer
5. In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.
Answer
Since radius = length of chord = 20 cm
=> △OAB is equilateral triangle
=> θ = 60° => l = rθ
=> l = 20 × 60° × Ï€/180° = 20Ï€/3
l = 20Ï€/3 cm
6. If in two circles, arcs of the same length subtend angles 60° and 75° at the centre. Find the ratio of their radii.
Answer
l = r1θ =r1 × 60 × Ï€/180° = Ï€r1/3
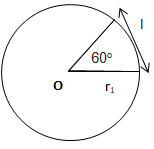
and l = r2θ = r2 × 75 × Ï€/180° = 5Ï€r2/12
since, l is same for both the circles
(Ï€/3)r1 = (5Ï€/12)r2 => r1 : r2 = 5 : 4
7. Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length.
(i) 10 cm
(ii) 15 cm
(iii) 21 cm
Answer
(i) r = 75cm, l = 10cm
We know, θ = l/r = 10/75 = 2/15 radians
(ii) r = 75cm, l = 15cm
We know, θ = l/r = 15/75 = 1/5 radians
(iii) r = 75cm , l = 21cm
We know, θ = l/r = 21/75 = 7/25 radians
6. If in two circles, arcs of the same length subtend angles 60° and 75° at the centre. Find the ratio of their radii.
Answer
l = r1θ =r1 × 60 × Ï€/180° = Ï€r1/3
and l = r2θ = r2 × 75 × Ï€/180° = 5Ï€r2/12
since, l is same for both the circles
(Ï€/3)r1 = (5Ï€/12)r2 => r1 : r2 = 5 : 4
7. Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length.
(i) 10 cm
(ii) 15 cm
(iii) 21 cm
Answer
(i) r = 75cm, l = 10cm
We know, θ = l/r = 10/75 = 2/15 radians
(ii) r = 75cm, l = 15cm
We know, θ = l/r = 15/75 = 1/5 radians
(iii) r = 75cm , l = 21cm
We know, θ = l/r = 21/75 = 7/25 radians