R.D. Sharma Solutions Class 10th: Ch 7 Statistics MCQ's

Chapter 7 Statistics R.D. Sharma Solutions for Class 10th Math MCQ's

Multiple Choice Questions

1. Which of the following is not a measure of central tendency ? 
(a) Median
(b) Median
(c) Mode
(d) Standard deviation 

Solution

Standard deviation is not a measure of central tendency
Hence , the correct option is c

2. The algebraic sum of the deviations of a frequency distribution from its mean is
(a) Always positive
(b) Always Negative
(c) 0
(d) A non – zero number

Solution

The algebraic sum of the deviation of a frequency distribution from its mean is zero .
Hence , the correct option is c. 

3. The arithmetic mean of 1,2,3,…,n is
(a) n+1/2
(b) n-1/2
(c) n/2
(d) n/2 + 1 

Solution

Arithmetic mean of 1,2,3,…,n
= 1+2+3+…+n/n
= n(n+1)/2/n
= n+1/2
Hence , the correct option is a .

4. For a frequency distribution, mean, median and mode are connected by the relation
(a) Mode = 3 Mean – 2 Median
(b) Mode = 2 median – 3 Mean
(c) Mode = 3 Median – 2 Mean
(d) Mode = 3 Median + 2 Mean

Solution

The relation between mean, median and mode is
Mode = 3 Median – 2 Mean 

Hence, the correct option is c .

5. Which of the following cannot be determined graphically ?
(a) Mean
(b) Median
(c) Mode
(d) None of these

Solution

‘Mean’ cannot be determined by graphically.
Hence, the correct option is a .

6. The median of a given frequency distribution is found graphically with the help of 

(a) Histogram
(b) Frequency curve
(c) Frequency Polygon
(d) Ogive

Solution

The median of a given frequency distribution is found graphically with the help of ‘ogive’ .
Hence , the correct option is d .

7. The mode of a frequency distribution can be determined graphically from
(a) Histogram
(b) Frequency polygon
(c) Ogive
(d) Frequency curve 

Solution

The mode of a frequency distribution can be determined from ‘’Histogram’’ .
Hence, the correct option is a.      

8. Mode is
(a) Least frequency value
(b) Middle most value
(c) Most frequent value
(d) None of these

Solution

Mode is ‘’ Most frequent value’’ .
Hence , the correct option is c .

9. The mean of n observation is x̅ . If the first item is increased by 1, second by 2 and so on, then the new mean is 

(a) x̅ + n
(b) x̅ + n/2
(c) x̅ + n+1/2
(d) None of these

Solution

Let x₁ , x₂ , x₃, …..,x_n be the n observations .
Mean = x̅ = x₁+x₂+…+x_n/n
⇒ x₁ + x₂ +x₃ + …+ x_n = n x̅
If the first item is increased by 1, second by 2 and so on .
Then, the new observations are x₁ + x₂ + 2 , x₃ + 3, …, x_n + n.
New mean = (x₁ + 1) + (x₂+2) + (x₃ + 3) + … +(x_n+n)/n
= x₁+ x₂ + x₃ + … + x_n + (1+2+3+…+n)
= n x̅ + (n(n+1)/2)/n
= x̅ + n+1/2
Hence , the correct answer is c .

10. One of the methods of determining mode is
(a) Mode = 2 median – 3 mean
(b) Mode = 2 median + 3 mean
(c) Mode = 3 median – 2 mean
(d) Mode = 3 median + 2 mean

Solution

We have ,
Mode = 3 median – 2 mean
Hence , the correct option is c .

11. If the mean of the following distribution is 2.6 , then the value of y is
Variable (x) : 1 2 3 4 5
Frequency     4 5 y 1 2

Solution

Now,
Mean = Σfx/ Σf
2.6/1 = 28 + 3y/12 + y
31.2 + 2.6y = 28 + 3y
0.4y = 3.2
y = 3.2/0.4
y = 8
Hence, the correct option is b .

12. The relationship between mean, median and mode for a moderately skewed distribution is
(a) Mode = 2 median – 3 mean
(b) Mode = median – 2 mean
(c) Mode = 2 median – mean
(d) Mode = 3 median – 2 mean

Solution

Mode = 3 median - 2 mean 

Hence, the correct option is d . 

13. The mean of a discrete frequency distribution x_i / f_i, i = 1,2,…,n is given by

Solution

The mean of discrete frequency distribution is
x̅ = Σf_ix_i/Σf_i
Hence, the correct option is a .

14. If the arithmetic mean of x, x+3, x+6, x+9, and x+12 is 10, the x =
(a) 1
(b) 2
(c) 6
(d) 4

Solution

The given observations are x, x+3, x+6, x+9, and x +12.
∴ Σ x = 5x + 30, n = 5, x̅ = 10
Now,
x̅ = Σx/n
10 = 5x + 30/5
50 = 5x + 30
5x = 20
x = 4
Hence, the correct option is d.

15. If the median of the data : 24,25,26,x+2x+3,30,31,34 is 27.5 , then x =
(a) 27
(b) 25
(c) 28
(d) 30

Solution

The given observations are 24, 25, 26, x + 2, x + 3, 30, 31, 34
Median = 27.5
Here, n = 8
Median = (n/2)^th term + (n/2 + 1)^th term / 2
27.5 = 4th term + 5 th term/2
27.5 = (x+2) + (x+3) / 2
27.5 = 2x + 5 / 2
2x + 5 = 55
2x = 50
x = 25
Hence , the correct option is b .

16. If the median of the data : 6,7,x-2, x,17,20 written ascending order is, 16 . Then x =
(a) 15
(b) 16
(c) 17
(d) 18

Solution

The given observations arranged in ascending order are
6,7,x-2,x,17,20
n = 6(even), median = 16
Median = (n/2)^th term + (n/2 +1)^th term/2
= 3rd term + 4th term/2
= x – 2 + x /2
= 2x – 2 / 2
= 16 = 2x – 2 / 2
= 2x – 2 = 32
x = 17
Hence the correct option is c.

17. The median of first 10 prime numbers is
(a) 11
(b) 12
(c) 13
(d) 14

Solution

First 10 prime numbers are 2 ,3 , 5 ,7 , 11 , 13 , 17, 19 , 23, 29 .
n = 10 (even)
Median = (n/2)th term + (n/2+1)th term
= 5th term + 6th term / 2
= 11 + 13 / 2
= 24/2
= 12
Hence, the correct option is b.

18. If the mode of the data : 64,60,48, x, 43, 34 is 43, then x + 3 

(a) 44
(b) 45
(c) 46
(d) 48

Solution

It is given that the mode of the given date is 43 . So, it is the value with the maximum frequency .
Now, this is possible only when x = 43. In this case, the frequency of the observation 43 would be 3.
Hence,
x + 3 = 46
Hence, the correct option is c .

19. If the mode of the data : 16, 15, 17, 16, 15, x, 19, 17, 14 is 15, then x =
(a) 15
(b) 16
(c) 17
(d) 19

Solution

It is given that the mode of the data is 15. So, it is the observation with the maximum frequency .
This is possible only when x = 15. In this case, the frequency of 15 would be 3.
Hence , the correct answer is a .

20. The mean of 1,3,4,5,7,4 is m. The numbers 3,2,2,4,3,3,p have mean m – 1 and median q. Then, p+q = 

(a) 4
(b) 5
(c) 6
(d) 7

Solution 

1,3,4,5,7,4
Mean = 1+3+4+5+7+4/6
= 24/6
= 4
Consider the numbers 3,2,2,4,3,3,p.
Mean = 3+2+2+4+3+3+p / 7.
⇒ 7× (4 – 1) = 17 + p
⇒ 21 = 17 + p
⇒ p = 4
Arranging the numbers 3,2,2,4,3,3,4 in ascending order, we have
2,2,3,3,3,4,4
Median = (n+1/2)^th term
q = (7+1/2)^th term
= (8/2)^th term
= 4^th term
q = 3
so,
p+q = 4 + 3
= 7
Hence , the correct option is d.

21. If the mean of frequency distribution is 8.1 and Σf_ix_i = 132 + 5k, Σf_i = 20, then k =

(a) 3

(b) 4
(c) 5
(d) 6

Solution

Given:
Σf_ix_i = 132 + 5k, Σf_i = 20 and mean = 8.1
Then,
Mean = Σf_ix_i / Σf_i
8.1 = 132 + 5k / 20
162 = 132 + 5k
5k = 30
k = 6
Hence , the correct option is d .

22. If the mean of 6,7,x,8,y,14 is 9, then
(a) x+y = 21
(b) x+y = 19
(c) x-y = 19
(d) x-y = 21

Solution

The given observation are 6,7,x,8,y,14.
Mean = 9 (Given)
⇒ 6+7+x+8+y+14 / 6 = 9
⇒ 35 + x + y = 54
⇒ x + y = 54 – 35 = 19
Hence , the correct option is b . 

23. 

Solution

24. If the mean of first n natural numbers is 5n/9 then n =
(a) 5
(b) 4
(c) 9
(d) 10

Solution

25. The arithmetic mean and mode of a data are 24 and 12 respectively , then its median is 
(a) 25
(b) 18
(c) 20
(d) 22

Solution

Given :
Mean = 24 and Mode = 12
We know that
Mode = 3 Median – 2 Mean
⇒ 12 = 3 median – 2 × 24
⇒ 3 median = 12 + 48 = 60
⇒ Median = 20

26. The mean of first n odd natural number is
(a) n+1/2
(b) n/2
(c) n
(d) n²

Solution

27. The mean of first n odd natural numbers is n²/81, then n =
(a) 9
(b) 81
(c) 27
(d) 18

Solution

28. If the difference of mode and median of a data is 24, then the difference of median and mean is
(a) 12
(b) 24
(c) 8
(d) 36

Solution

Given :
Mode – Median = 24
We know that
Mode = 3 median – 2 mean
Now,
Mode – median = 2(Median – Mean)
⇒ 24 = 2(Median – Mean)
⇒ Median – Mean = 12
 29. If the arithmetic mean , 7,8,x,11,14 is x, then x = 
(a) 9
(b) 9.5
(c) 10
(d) 10.5

Solution

The given observations are 7,8,x,11,14 .
Mean = x (Given)
Now,
Mean = 7+8+x+11+14 / 5
⇒ x = 40+x / 5
⇒ 5x = 40 + x
⇒ 4x = 40
⇒ x = 10

30. If the mode of a series exceeds its mean by 12, then mode exceeds the median by
(a) 4
(b) 8
(c) 6
(d) 10

Solution

Given: Mode – Mean = 12
We know that
Mode = 3 median – 2 Mean
∴ Mode – Mean = 3(Median – Mean)
⇒ 12 = 3(Median – Mean)
⇒ Median – Mean = 4 …(1)
Again ,
Mode = 3 Median – 2 Mean
⇒ 2 Mode = 6 Median – 4 Mean
⇒ Mode – Mean + Mode = 6 Median – 5 Mean
⇒ 12 + (Mode – Median) = 5(Median – Mean)
⇒ 12 + (Mode – Median) = 20 [Using (1)]
⇒ Mode – Median = 20 – 12 = 8

31. If the mean of first n natural number is 15, then n =
(a) 15
(b) 30
(c) 14
(d) 29

Solution



32.

Solution

33. 

Solution

34. 

(a) 23 

(b) 24
(c) 27
(d) 25

Solution

35. If 35 is removed from the data: 30,34,35,36,37,38,39,40 then the median increased by
(a) 2
(b) 1.5
(c) 1
(d) 0.5

Solution

36. While computing mean of grouped data, we assume that the frequencies are
(a) Evenly distributed over all the classes.
(b) Centred at the class marks of the classes.
(c) Centred at the upper limit of the classes .
(d) Centred at the lower limit of the classes .

Solution

We know that while computing the mean of a grouped data, the frequencies are centered at the class marks of the classes . 

37.

Solution

38. For the following distributions :
Class :  0-5  5-10  10-15  15-20  20-25
Frequency : 10 15  12  20   9
The sum of the lower limits of the median and modal class is
(a) 15
(b) 25
(c) 30
(d) 35

Solution
 

Here, N = 66.

∴ N/2 = 33, which lies in the interval 10-15. 

So, the lower limit of the median class is 10.
The highest frequency is 20, which lies in the interval 15-20.
Therefore, the lower limit of modal class is 15.
So, the required sum is 10 +15 = 25 .

39. For the following distribution :
Below: 10   20   30   40   50   60
Number of students : 3  12  27  57   75   80
the modal class is
(a) 10-20
(b) 20-30
(c) 30-40
(d) 50-60

Solution 

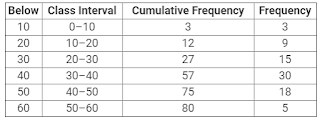
Here, N = 80 

∴ N/2 = 40, which lies in the interval 30-40.
Therefore, the modal class is 30-40.

40. Consider the following frequency distribution :

Class: 65-85  85-105  105-125  125-145  145-165  165-185  185-205
Frequency : 4 5 13 20 14 7 4
The difference of the upper limit of the median class and the lower limit of the modal class is :

Solution

Here, N = 67
∴ N/2 = 33.5, which lies in the interval 125-145.
Therefore, the lower limit of the median class is 125.
The highest frequency is 20, which lies in the interval 125-145.
Therefore, the upper limit of modal class is 145.
So, the required difference is 145-125 = 20.

41.  

Solution

The given formula represents the formula to find the mean by assumed mean method . 

Here, d_i = x_i – a where xi is the ith observation and a is assumed mean .
So, d_i’s are the deviation from a of mid – points of the classes .

42. The abscissa of the point of intersection of less than type and of the more than type cumulative frequency curves of a grouped data gives its
(a) Mean
(b) Median
(c) Mode
(d) All the three above

Solution

The less than ogive and more than ogive when drawn on the same graph intersect at a point . From this point, if we draw a perpendicular on the x-axis, the point at which it cuts the x-axis gives us the median.

 Thus, the abscissa of the point if intersection of less than type and of the more than type cumulative curves of a grouped data gives its median.

43. Consider the following frequency distribution :
Class:  0-5  6-11  12-17  18-23   24-29
Frequency: 13  10  15   8   11
The upper limit of the median class is
(a) 17
(b) 17.5
(c) 18
(d) 18.5 

Solution

The given classes in the table are non-continuous. So , we first make the classes continuous by adding 0.5 to the upper limit and substracting 0.5 from the lower limit in each class .    

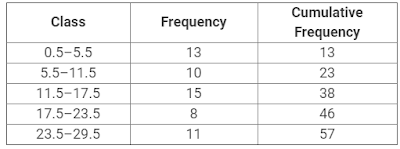Now, from the table we see that N = 57. 

So, N/2 = 57/2 = 28.5

28.5 lies in the class 11.5 – 17.5

The upper limit of the interval 11.5-17.5 is 17.5