Chapter 18 Surface Area and Volume of a Cuboid and Cube R.D. Sharma Solutions for Class 9th MCQ's
Multiple Choice Questions
1. If A 1 ,A 2 ,and A 3 denote the areas of three adjacent faces of a cubiod, then its volume is
(a) A 1 A 2 A 3
(b) 2A 1 A 2 A 3
(c ) √(A 1 A 2 A 3 )
(d) ∛(A 1 A 2 A 3 )

2. The length of the longest rod that can be fitted in a cubical vessel of edge 10 cm long, is
(a) 10 cm
(b) 10√2 cm(c) 10√3 cm
(d) 20 cm
Solution

3. If l is the length of a diagonal of a cube of volume V, then
(a) 3V = l3(b) √3V = l3
(c) 3√3V = 2l3
(d) 3√3V = l3
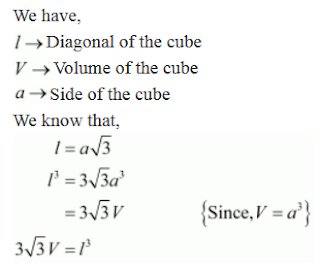
4. Three equal cubes are placed adjacently in a row. The ratio of the total surface area of the resulting cuboid to that of the sum of the surface areas of three cubes, is
(a) 7 : 9
(b) 49 : 81
(c) 9 : 7
(d) 27 : 23
Solution

5. If V is the volume of a cuboid of dimensions x, y, z and A is its surface area, then A/V
(a) x2y2z2
(b) 1/2 (1/xy + 1/yz + 1/zx)(c) (1/x + 1/y + 1/z)
(d) 1/xyz
Solution

6. The sum of the length, breadth and depth of a cuboid is 19 cm and its diagonal is 5√5 cm. Its surface area is
(a) 361 cm2(b) 125 cm2
(c) 236 cm2
(d) 486 cm2

7. If the length of a diagonal of a cube is 8√3 cm, then its surface area is
(a) 512 cm2(b) 384 cm2
(c) 192 cm2
(d) 768 cm2
Solution

8. If each edge of a cube is increased by 50%, the percentage increase in its surface area is
(a) 50 %
(b) 75 %
(c) 100 %
(d) 125 %
Solution

9. If the volumes of two cubes are in the ratio 8: 1, then the ratio of their edges is
(a) 8 : 1(b) 2√2:1
(c) 2 : 1
(d) none of these
Solution

10.The volume of a cube whose surface area is 96 cm2, is
(a) 16√2cm3(b) 32 cm3
(c) 64 cm3
(d) 216 cm3
Solution

11. The length, width and height of a rectangular solid are in the ratio of 3 : 2 : 1. If the volume of the box is 48cm3, the total surface area of the box is
(a) 27 cm2(b) 32 cm2
(c) 44 cm2
(d) 88 cm2
Solution

12. A cube whose volume is 1/8 cubic centimeter is placed on top of a cube whose volume is 1 cm3. The two cubes are then placed on top of a third cube whose volume is 8 cm3. The height of the stacked cubes is
(a) 3.5 cm(b) 3 cm
(c) 7 cm
(d) none of these
Solution

13. If the areas of the adjacent faces of a rectangular block are in the ratio 2 : 3 : 4 and its volume is 9000 cm3, then the length of the shortest edge is
(a) 30 cm(b) 20 cm
(c) 15 cm
(d) 10 cm
Solution

14. If each edge of a cube, of volume V, is doubled, then the volume of the new cube is
(a) 2 V
(b) 4 V
(c) 6 V
(d) 8 V
Solution

15. If each edge of a cuboid of surface area S is doubled, then surface area of the new cuboid is
(a) 2 S
(b) 4 S
(c) 6 S
(d) 8 S
Solution

16. The area of the floor of a room is 15 m2. If its height is 4 m, then the volume of the air contained in the room is
(a) 60 dm3(b) 600 dm3
(c) 6000 dm3
(d) 60000 dm3
Solution

17. The area of the floor of a room is 15 m2. If its height is 4 m, then the volume of the air contained in the room is
(a) 60 dm3(b) 600 dm3
(c) 6000 dm3
(d) 60000 dm3
Solution

18. 10 cubic metres clay is uniformly spread on a land of area 10 ares. the rise in the level of the ground is
(a) 1 cm
(b) 10 cm
(c) 100 cm
(d) 1000 cm
Solution

19. Volume of a cuboid is 12 cm3. The volume (in cm3) of a cuboid whose sides are double of the above cuboid is
(a) 24(b) 48
(c) 72
(d) 96
Solution

20. If the sum of all the edges of a cube is 36 cm, then the volume (in cm3) of that cube is
(a) 9(b) 27
(c) 219
(d) 729
Solution

21. The number of cubes of side 3 cm that can be cut from a cuboid of dimensions 10 cm×9 cm×6 cm, is
(a) 9
(b) 10
(c) 18
(d) 20
Solution

22. On a particular day, the rain fall recorded in a terrace 6 m long and 5 m broad is 15 cm. The quantity of water collected in the terrace is
(a) 300 litres
(b) 450 litres
(c) 3000 litres
(d) 4500 litres
Solution

