Chapter 17 Construction R.D. Sharma Solutions for Class 9th Exercise 17.2
Exercise 17.2
1. Draw an angle and label it as ∠BAC. Construct another angle, equal to ∠BAC.
Solution
We are asked to draw an angle BAC and construct another angle equal to angle BAC
We follow a certain algorithm to construct the angle .

STEP 1: Draw an angle of any measure, and label it as ∠BAC. We have to construct another angle equal to this angle.
STEP 2: Draw a ray LN.
STEP 3: With centre A and radius equal to AB, draw an arc cutting the ray AC at point D.
STEP 4: With centre L and taking the same radius as AB, draw an arc cutting the ray LN at point P.
STEP 5: With centre P, and radius equal to BD, draw an arc intersecting the arc drawn in step 4, at point M.
STEP 6: Draw ray LM.
∠MLN = ∠BAC
2. Draw an obtuse angle. Bisect it. Measure each of the angles so obtained.
Solution
We are asked to construct an angle and bisect it and measure each angle
We will follow a certain algorithm to construct
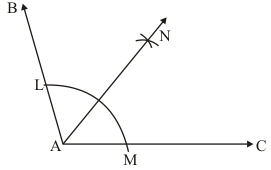
STEP 1: Draw an obtuse angle of any measure. For example take 100 degrees. And label it as ∠BAC.
STEP 2: With centre as A, and radius of any measure, draw an arc intersecting the ray AB and AC, at L and M respectively.
STEP 3: With centre M and radius greater than half of LM, draw an arc inside the cone.
STEP 4: With centre L and taking the same radius as in STEP 3, draw another arc intersecting the previous one at N.
STEP 5: Draw the ray AN. This is the angle bisector of ∠BAC.
After measurement, we can find out that, ∠BAN =∠NAC = 50°∠BAN =∠NAC = 50°.
3. Using your protractor, draw an angle of measure 108°. With this angle as given, draw an angle of 54°.
Solution
We are asked to draw an angle of 108°, using protractor and obtain an angle of 54°
We will follow certain algorithm for this construction

STEP 1: Using the protractor, draw ∠ABC of measure 108°.
STEP 2: With centre B, and taking any radius, draw an arc, intersecting the ray BA and the ray BC at point D and E respectively.
STEP 3: With D and E as centre and radius greater than half of DE, draw arcs to intersect each other at say F.
STEP 4: Draw the ray BF. This is the angle bisector of ∠ABC. So ∠FBC = 54°.
STEP 5: With centre B and taking any radius, draw an arc intersecting the ray BF and the ray BC at G and H respectively.
STEP 6: Draw a ray MN.
STEP 7: With centre M and taking the same radius as in STEP 5, draw an arc intersecting the ray MN at point P.
STEP 8: With centre P and taking radius equal to HG, draw an arc intersecting the arc drawn in STEP 7, at point L.
STEP 9: Draw the ray ML.
∠LMN is the desired angle of measure 54°.
4. Using protractor, draw a right angle. Bisect it to get an angle of measure 45°.
Solution
We are asked to construct an angle of 90° using protractor and bisect it
We will follow the following algorithm to construct this figure
Steps of Construction
STEP 1: Using the protractor, draw a right angle and label it as ∠ABC.
STEP 2: With centre as B, draw an arc of any radius, intersecting the ray BA at D and the ray BC at E.
STEP 3: With centre as D, and taking radius greater than half of DE, draw an arc inside the ∠ABC.
STEP 4: With centre as E, and taking the same radius, draw another arc, intersecting the previous arc at F.
STEP 5: Draw the ray BF.
∠ABF = ∠FBC = 45°
5. Draw a linear pair of angles. Bisect each of the two angles. Verify that the two bisecting rays are perpendicular to each other.
Solution
We are asked to draw a linear pair of angles and bisect each of them and verify that the two bisecting rays are perpendicular to each other
We follow the following algorithm for construct

STEP 1: Draw a linear pair of angles and label them as ∠ABD and ∠DBC.
STEP 2: Draw an arc of sufficient radius, intersecting the ray BA, ray BD and the ray BC at points G, H and I respectively.
STEP 3: With centre I and H and radius greater than half of HI draw arcs intersecting each other at point say F.
STEP 4: With centre G and H as centres and radius as more than half of GH, draw arcs intersecting each other at point say E.
STEP 5: Draw the ray BE and the ray BF.
After the measurement, it can be verified that ∠EBF is a right angle.
Hence the ray BE and the ray BF are perpendicular to each other.
6. Draw a pair of vertically opposite angles. Bisect each of the two angles. Verify that the bisecting rays are in the same line.
Solution
We are asked to draw a pair of vertically opposite angles bisect each of them and verify that the two of them are in the sane line
We will follow the following algorithm for construction.

Steps of construction
STEP 1: Draw a pair of vertically opposite angles, ∠ABC and ∠DBE.
STEP 2: With B as a centre, and taking any radius, draw an arc intersecting the ray BD and the ray BE at points F and G, respectively.
STEP 3: With G as a centre, and radius greater than half of FG, draw an arc inside of ∠DBE.
STEP 4: With F as a centre, and taking the same radius as in STEP 3, draw an arc intersecting the arc drawn in STEP 3, at N.
STEP 5: Draw the ray BN.
STEP 6: With B as a centre, and taking any radius, draw an arc intersecting the ray BA and the ray BC at points H and K, respectively.
STEP 7: With H as a centre, and radius greater than half of HK, draw an arc inside of ∠ABC.
STEP 8: With K as a centre, and taking the same radius as in STEP 7, draw an arc intersecting the arc drawn in STEP 7, at M
STEP 9: Draw the ray BM
After measuring the ∠MBN, it can be verified that the bisecting rays BM and BN are in the same line.
7. Using ruler and compasses only, draw a right angle.
Solution
We have to draw a right angle using ruler and compasses only
We use the following algorithm for the construction

STEP 1: Draw a ray BC.
STEP 2: With B as a centre, and taking convenient radius, draw an arc, intersecting the ray BC at point N.
STEP 3: With N as a centre, and taking the same radius, draw an arc cutting the previous arc at M.
STEP 4: With M as a centre, and the same radius, draw an arc cutting the arc drawn in STEP2 at L.
STEP 5: With M and L as centre and the same radius draw arcs intersecting at a point say A.
STEP 6: Draw the ray BA.
∠ABC is a right angle.
8. Using ruler and compasses only, draw an angle of measure 135°.
We have to draw an angle of 135° using ruler and compasses only
We follow the following algorithm for the construction
Steps of construction
The below given steps will be followed to construct an angle of 135°.
STEP 1: Take the given ray PQ. Extend PQ on the opposite side of Q. Draw a semi-circle of some radius taking point P as its centre, which intersects PQ at R and W.
STEP 2: Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at S.
STEP 3: Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T (see figure).
STEP 4: Taking S and T as centre, draw an arc of same radius to intersect each other at U.
STEP 5: Join PU. Let it intersect the arc at V. Taking V and W as centre and with radius more than 1/2VW , draw arcs to intersect each other at X. Join PX, which is the required ray making 135° with the given line PQ.
9. Using a protractor, draw an angle of measure 72°. With this angle as given, draw angles of measure 36° and 54°.
Solution
Using protractor we have to draw an angle of 72° and considering this angle given draw an angle of 36° and 54°
For this construction we will follow the following algorithm

Steps of Construction
STEP 1: Draw ∠ABC of measure 72°, using protractor.
STEP 2: Bisect ∠ABC. Let BD be the bisecting ray.
∠ABD = ∠DBC = 36°
∠EBD = 1/2 ∠ABD
= 1/2 × 36°
= 18°
Thus,
∠EBC = ∠EBD + ∠ABD
= 36° + 18°
= 54°
Thus, ∠DBC = 36° and ∠EBC = 54° are the required angles .
10. Construct the following angles at the initial point of a given ray and justify the construction.
(i) 45°
(ii) 90°
Solution
(i) Construction of 45°.
The below given steps will be followed to construct an angle of 45°.
STEP 1: Take the given ray PQ. Draw an arc of some radius taking point P as its centre, which intersects PQ at R.
STEP 2: Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at S.
STEP 3: Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T (see figure).
STEP 4: Taking S and T as centre, draw an arc of same radius to intersect each other at U.
STEP 5: Join PU. Let it intersect the arc at point V.
STEP 6: From R and V, draw arcs with radius more than 1/2 RV to intersect each other at W. Join PW.
PW is the required ray making 45° with PQ.

We can justify the construction, if we can prove ∠WPQ = 45°.
For this, join PS and PT.


(ii) Construction of 90°.
STEP 1: Take the given ray PQ. Draw an arc of some radius taking point P as its centre, which intersects PQ at R.
STEP 2: Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at S.
STEP 3: Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T (see figure).
STEP 4: Taking S and T as centre, draw an arc of same radius to intersect each other at U.
STEP 5: Join PU, which is the required ray making 90° with the given ray PQ.

Justification of Construction:
We can justify the construction, if we can prove ∠UPQ = 90°.For this, join PS and PT.

∴ ∠UPS = 1/2 ∠TPS = 1/2 × 60° = 30°
Also, ∠UPQ = ∠SPQ + ∠UPS
= 60° + 30°
= 90°
11. Construct the angles of the following measurements:
(i) 30°
(ii) 75°
(iii) 105°
(iv) 135°
(v) 15°
(vi)22½°
Solution
(i) 30°
The below given steps will be followed to construct an angle of 30°.
Step I: Draw the given ray PQ. Taking P as centre and with some radius, draw an arc of a circle which intersects PQ at R.
Step II: Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at point S.
Step III: Taking R and S as centre and with radius more than 1/2 RS, draw arcs to intersect each other at T. Join PT which is the required ray making 30° with the given ray PQ.

(ii) 75°
The below given steps will be followed to construct an angle of 75°.Step I: Take the given ray PQ. Draw an arc of some radius taking point P as its centre, which intersects PQ at R.
Step II: Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at S.
Step III: Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T (see figure).
Step IV: Taking S and T as centre, draw an arc of same radius to intersect each other at U.
Step V: Join PU. Let it intersect the arc at V. Taking S and V as centre, draw arcs with radius more than 1/2 SV. Let those intersect each other at W. Join PW which is the required ray making 75° with the given ray PQ.

The angle so formed can be measured with the help of a protractor. It comes to be 75º.
(iii) 105°
The below given steps will be followed to construct an angle of 105°.Step I: Take the given ray PQ. Draw an arc of some radius taking point P as its centre, which intersects PQ at R.
Step II: Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at S.
Step III: Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T (see figure).
Step IV: Taking S and T as centre, draw an arc of same radius to intersect each other at U.
Step V: Join PU. Let it intersect the arc at V. Taking T and V as centre, draw arcs with radius more than 1/2 TV. Let these arcs intersect each other at W. Join PW which is the required ray making 105° with the given ray PQ.

(iv) 135°
We follow the following algorithm for the construction

Steps of construction
The below given steps will be followed to construct an angle of 135°.
Step I: Take the given ray PQ. Extend PQ on the opposite side of Q. Draw a semi-circle of some radius taking point P as its centre, which intersects PQ at R and W.
Step II: Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at S.
Step III: Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T (see figure).
Step IV: Taking S and T as centre, draw an arc of same radius to intersect each other at U.
Step V: Join PU. Let it intersect the arc at V. Taking V and W as centre and with radius more than 1/2 VW, draw arcs to intersect each other at X. Join PX, which is the required ray making 135°with the given line PQ.
(v) 15°
The below given steps will be followed to construct an angle of 15°.
Step I: Draw the given ray PQ. Taking P as centre and with some radius, draw an arc of a circle which intersects PQ at R.
Step II: Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at point S.
Step III: Taking R and S as centre and with radius more than 1/2 RS, draw arcs to intersect each other at T. Join PT.
Step IV: Let it intersect the arc at U. Taking U and R as centre and with radius more than 1/2 RU, draw an arc to intersect each other at V. Join PV which is the required ray making 15° with the given ray PQ.

(vi)22½°
The below given steps will be followed to construct an angle of 22½°.
Step I: Take the given ray PQ. Draw an arc of some radius, taking point P as its centre, which intersects PQ at R.
Step II: Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at S.
Step III: Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T (see figure).
Step IV: Taking S and T as centre, draw an arc of same radius to intersect each other at U.
Step V: Join PU. Let it intersect the arc at point V.
Step VI: From R and V, draw arcs with radius more than 1/2 RV to intersect each other at W. Join PW.
Step VII: Let it intersect the arc at X. Taking X and R as centre and radius more than 1/2 RX, draw arcs to intersect each other at Y.
Step VIII: Joint PY which is the required ray making 22½° with the given ray PQ.



